题目内容
如图，在△ABC中，D、E分别是边AB、AC上的点，DE∥BC，AD：DB=1：2，S△ADE=1，则S四边形BCED的值为考点：相似三角形的判定与性质
专题：
分析：如图，证明△ADE∽△ABC，得到
=(
)2，求出
=
，得到S△ABC=9S△ADE=9，进而得到
S四边形BCED的值=9-1=8，即可解决问题．
| S△ADE |
| S△ABC |
| AD |
| AB |
| AD |
| AB |
| 1 |
| 3 |
S四边形BCED的值=9-1=8，即可解决问题．
解答：解：如图，∵DE∥BC，
∴△ADE∽△ABC，
∴
=(
)2，而
=
，
∴
=
，S△ABC=9S△ADE=9，
∴S四边形BCED的值=9-1=8，
故答案为8．
解：如图，∵DE∥BC，∴△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| AD |
| DB |
| 1 |
| 2 |
∴
| AD |
| AB |
| 1 |
| 3 |
∴S四边形BCED的值=9-1=8，
故答案为8．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；应牢固掌握相似三角形的判定及其性质．
练习册系列答案
相关题目
在四边形ABCD中，AB∥CD，AD∥BC，点E是线段BC的中点，F点在边DC上，AE平分∠BAF．
如图，⊙O的直径AB与弦CD互相垂直，垂足为点E，BF∥CD，BF与弦AD的延长线相交于点F，且AD=3，cos∠BCD=
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x．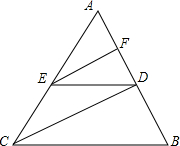
如图，在△ABC中，EF∥CD，DE∥BC，求证：AF•BD=AD•FD．
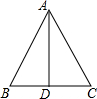若正三角形的边长为2
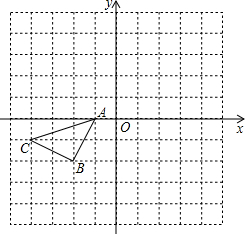如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：