题目内容
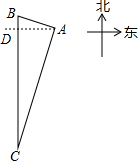 如图,某国3艘炮艇正追袭5条中国渔船,“中国渔政310”船(用“A”表示)接到陆地指挥中心(用“B”表示)命令疾速驰救中国渔船,渔船(用“C”表示)位于陆地指挥中心正南方向.经测定AB=
如图,某国3艘炮艇正追袭5条中国渔船,“中国渔政310”船(用“A”表示)接到陆地指挥中心(用“B”表示)命令疾速驰救中国渔船,渔船(用“C”表示)位于陆地指挥中心正南方向.经测定AB=| 6 |
| 24 |
| 18 |
考点:解直角三角形的应用-方向角问题
专题:
分析:过点A作AD⊥BC于点D,根据锐角三角函数的定义即可得出结论.
解答: 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,
∵AB=
海里,BC=
海里,AC=
海里,∠BAC=90°,
∴sin∠B=
=
,即
=
,
解得AD=
(海里).
答:A到BC的距离是
海里.
 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,∵AB=
| 6 |
| 24 |
| 18 |
∴sin∠B=
| AC |
| BC |
| AD |
| AB |
| ||
|
| AD | ||
|
解得AD=
3
| ||
| 4 |
答:A到BC的距离是
3
| ||
| 4 |
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
小明由等积式5x=6y写了以下比例式:①
=
;②
=
;③
=
;④
=
,则小明写出的比例式中正确的是( )
| y |
| x |
| 5 |
| 6 |
| x |
| y |
| 5 |
| 6 |
| x |
| 6 |
| y |
| 5 |
| 5 |
| x |
| y |
| 6 |
| A、①③ | B、②③ | C、②④ | D、③④ |
 如图,画AE⊥DC,DF⊥BC,垂足分别为点E,F.
如图,画AE⊥DC,DF⊥BC,垂足分别为点E,F. 如图,⊙O的直径AB与弦CD互相垂直,垂足为点E,BF∥CD,BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=
如图,⊙O的直径AB与弦CD互相垂直,垂足为点E,BF∥CD,BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=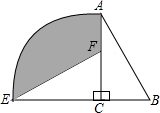 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB= 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.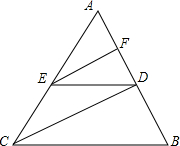 如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.
如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.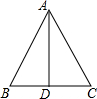 若正三角形的边长为2
若正三角形的边长为2