题目内容
13.解不等式组$\left\{\begin{array}{l}{1-3(x-1)<8-x①}\\{\frac{x-3}{2}+3≥x+1②}\end{array}\right.$并写出该不等式组的整数解.分析 先求出每个不等式的解集,再求出不等式组的解集,最后求出答案即可.
解答 解:$\left\{\begin{array}{l}{1-3(x-1)<8-x①}\\{\frac{x-3}{2}+3≥x+1②}\end{array}\right.$,
∵解不等式①得:x>-2,
解不等式②得:x≤1,
∴不等式组的解集为-2<x≤1,
∴不等式组的整数解为-1,0,1.
点评 本题考查了解一元一次不等式组,不等式组的整数解的应用,能求出不等式组的解集是解此题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
3.一项工程甲队单独完成需要x天,乙队单独完成所用的时间比甲队单独完成所用的时间多5天,现在先由乙队做x天,剩下由甲、乙两队合作2天完成,求x的值,根据题意列方程正确的是( )
| A. | $\frac{2}{x}$+$\frac{x+2}{x+5}$=1 | B. | $\frac{2}{x}$+$\frac{x}{x+5}$=1 | C. | $\frac{2}{x}$+$\frac{x}{x-5}$=1 | D. | $\frac{2}{x}$+$\frac{x+2}{x-5}$=1 |
18.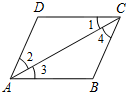 如图所示,下列推理及所注理由错误的是( )
如图所示,下列推理及所注理由错误的是( )
 如图所示,下列推理及所注理由错误的是( )
如图所示,下列推理及所注理由错误的是( )| A. | ∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行) | |
| B. | ∵AB∥CD,∴∠1=∠3(两直线平行,内错角相等) | |
| C. | ∵AD∥BC,∴∠2=∠4(两直线平行,内错角相等) | |
| D. | ∵∠2=∠4,∴AB∥CD(内错角相等,两直线平行) |
2. 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
 如图,⊙O的直径AB⊥弦CD,垂足为点E,连接AC,若CD=2$\sqrt{3}$,∠A=30°,则⊙O的半径为2.
如图,⊙O的直径AB⊥弦CD,垂足为点E,连接AC,若CD=2$\sqrt{3}$,∠A=30°,则⊙O的半径为2.