题目内容
2. 如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )
如图,⊙O中,OA⊥BC,AD∥OC,∠AOC=40°,则∠B的度数为( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
分析 由平行线的性质得出∠A=∠AOC=40°,由对顶角相等得出∠2=∠1=50°,由垂径定理得出$\widehat{AB}=\widehat{AC}$,得出∠AOB=∠AOC=40°,由圆周角定理求出∠D,再由三角形内角和定理即可得出结果.
解答 解:连接OB,如图所示:
∵AD∥OC,
∴∠A=∠AOC=40°,
∵OA⊥BC,
∴∠1=∠2=90°-∠A=90°-40°=50°,$\widehat{AB}=\widehat{AC}$,
∴∠AOB=∠AOC=40°,
∴∠D=$\frac{1}{2}$∠AOB=20°,
∴∠B=180°-50°-20°=110°;
故选:B.
点评 本题考查了垂径定理、圆周角定理、平行线的性质等知识;熟练掌握垂径定理是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
12. 如下图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,则这个矩形对角线的长是( )
如下图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,则这个矩形对角线的长是( )
 如下图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,则这个矩形对角线的长是( )
如下图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,则这个矩形对角线的长是( )| A. | 2.5 | B. | 5 | C. | 6 | D. | 7.5 |
14.用48m长的篱笆在空地上围成一个正六边形绿地,绿地的面积是( )
| A. | $96\sqrt{3}$m2 | B. | $64\sqrt{3}$m2 | C. | $32\sqrt{3}$m2 | D. | $16\sqrt{3}$m2 |
11. 如图,DE是△ABC的中位线,若BC=8,则DE的长为( )
如图,DE是△ABC的中位线,若BC=8,则DE的长为( )
 如图,DE是△ABC的中位线,若BC=8,则DE的长为( )
如图,DE是△ABC的中位线,若BC=8,则DE的长为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
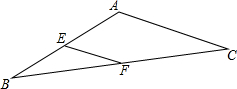 如图在△ABC中,AB=5,BC=7,EF是的中位线,则EF的长度范围是1<EF<6.
如图在△ABC中,AB=5,BC=7,EF是的中位线,则EF的长度范围是1<EF<6. 学校新年联欢会上某班矩形有奖竞猜活动,猜对问题的同学即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖品分别为台灯、笔记本、签字笔.请问:
学校新年联欢会上某班矩形有奖竞猜活动,猜对问题的同学即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖品分别为台灯、笔记本、签字笔.请问: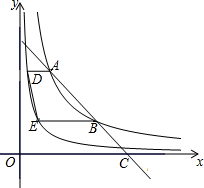 如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为$\frac{9}{2}$.
如图,在平面直角坐标系中,一条直线与反比例函数y=$\frac{8}{x}$(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为$\frac{9}{2}$.