题目内容
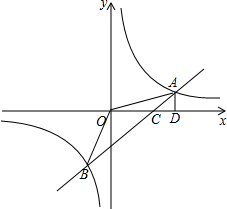 如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.(1)求一次函数y=kx+b及反比例函数的解析式;
(2)求△AOB的面积.
(3)根据图象回答:当x取何值时,反比例函数的值大于一次函数y=kx+b的值?
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先由OC=CD=2,可得OD=OC+CD=4,C(2,0),由S△OAD=4,根据三角形面积公式求出AD=2,那么A(4,2).再将A(4,2),C(2,0)代入y=kx+b,利用待定系数法求出一次函数解析式;设反比例函数的解析式为y=
,将A(4,2)代入y=
,利用待定系数法求出反比例函数的解析式;
(2)先解方程组
,求出B点坐标,再根据△AOB的面积=△AOC的面积+△BOC的面积,计算即可求解;
(3)根据图象,反比例函数落在一次函数上方的部分对应的x的值即为所求.
| m |
| x |
| m |
| x |
(2)先解方程组
|
(3)根据图象,反比例函数落在一次函数上方的部分对应的x的值即为所求.
解答:解:(1)∵OC=CD=2,
∴OD=OC+CD=4,C(2,0),
∵S△OAD=4,
∴
×4×AD=4,
∴AD=2,
∴A(4,2).
将A(4,2),C(2,0)代入y=kx+b,
得
,解得
,
∴一次函数解析式为y=x-2;
设反比例函数的解析式为y=
,
将A(4,2)代入,得2=
,
解得m=8,
∴反比例函数的解析式为y=
;
(2)由
,解得
,
,
∵A(4,2),
∴B(-2,-4),
∴△AOB的面积=△AOC的面积+△BOC的面积
=
×2×2+
×2×4
=6;
(3)根据图象可知,当x<-2或0<x<4时,反比例函数的值大于一次函数y=kx+b的值.
∴OD=OC+CD=4,C(2,0),
∵S△OAD=4,
∴
| 1 |
| 2 |
∴AD=2,
∴A(4,2).
将A(4,2),C(2,0)代入y=kx+b,
得
|
|
∴一次函数解析式为y=x-2;
设反比例函数的解析式为y=
| m |
| x |
将A(4,2)代入,得2=
| m |
| 4 |
解得m=8,
∴反比例函数的解析式为y=
| 8 |
| x |
(2)由
|
|
|
∵A(4,2),
∴B(-2,-4),
∴△AOB的面积=△AOC的面积+△BOC的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=6;
(3)根据图象可知,当x<-2或0<x<4时,反比例函数的值大于一次函数y=kx+b的值.
点评:此题考查了反比例函数与一次函数的交点问题,三角形的面积,利用待定系数法求函数的解析式,难度适中.利用数形结合与方程思想是解题的关键.

练习册系列答案
相关题目
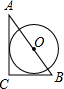 已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )
已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中,真命题是( )
| A、如果|a|=1,那么a=1 |
| B、2的平方根是根号2 |
| C、平行于同一直线的两直线平行 |
| D、三角形的一个外角大于三角形任意一个内角 |
抛物线y=2x2+bx+c的顶点坐标是(-1,-2),则b、c的值分别是( )
| A、-1,-2 | B、4,-2 |
| C、-4,0 | D、4,0 |
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AE:AC=3:4,AD=6,则BD等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AE:AC=3:4,AD=6,则BD等于( )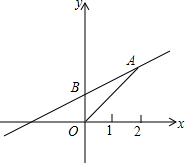 如图,已知平面直角坐标系xOy,直线y=
如图,已知平面直角坐标系xOy,直线y=