题目内容
用两种不同的方法解方程:x(x-2)=3.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:方程去括号整理后,利用因式分解法求出解即可;方程整理后利用配方法求出解即可.
解答:解:法1:方程整理得:x2-2x-3=0,
分解因式得:(x-3)(x+1)=0,
可得x-3=0或x+1=0,
解得:x1=3,x2=-1;
法2:方程整理得:x2-2x=3,
配方得:x2-2x+1=4,即(x-1)2=4,
开方得:x-1=2或x-1=-2,
解得:x1=3,x2=-1.
分解因式得:(x-3)(x+1)=0,
可得x-3=0或x+1=0,
解得:x1=3,x2=-1;
法2:方程整理得:x2-2x=3,
配方得:x2-2x+1=4,即(x-1)2=4,
开方得:x-1=2或x-1=-2,
解得:x1=3,x2=-1.
点评:出此题考查了解一元二次方程-因式分解法与配方法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
计算4x2•x3的结果是( )
| A、4x6 |
| B、4x5 |
| C、x6 |
| D、x5 |
将抛物线y=2(x+4)2-3的对称轴是( )
| A、直线x=4 |
| B、直线x=-4 |
| C、直线x=3 |
| D、直线x=-3 |
 在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.
在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.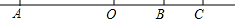 如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒)
如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒) 如图,两个三角形摆成如图所示的形状,其中EC⊥BC于点C,点D在AC边上,DE∥BC,若∠1=155°,则∠2的度数为
如图,两个三角形摆成如图所示的形状,其中EC⊥BC于点C,点D在AC边上,DE∥BC,若∠1=155°,则∠2的度数为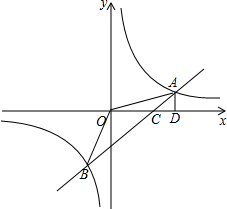 如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.