题目内容
已知关于x的一元二次方程x2-2x+1=m.
(1)若m是一个大于5而小于10的整数,且方程的两个根都是有理数,求m的值和它的另一个根;
(2)若方程x2-2x-m+1=0有两个不相等的实数根,试判断另一个关于x的方程x2-(m-2)x+1-2m=0的根的情况.
(1)若m是一个大于5而小于10的整数,且方程的两个根都是有理数,求m的值和它的另一个根;
(2)若方程x2-2x-m+1=0有两个不相等的实数根,试判断另一个关于x的方程x2-(m-2)x+1-2m=0的根的情况.
考点:一元二次方程的整数根与有理根
专题:
分析:(1)根据题意结合方程有两个有理根得出m=9,进而求出即可;
(2)利用根的判别式得出m的取值范围,进而得出答案.
(2)利用根的判别式得出m的取值范围,进而得出答案.
解答:解:(1)∵x2-2x+1=m
∴(x-1)2=m,
∵m是一个大于5而小于10的整数,且方程的两个根都是有理数,
∴m=9,
∴x-1=±3,
解得:x1=4,x2=-2,
故m的值为9和它的另一个根为2或4;
(2)∵方程x2-2x-m+1=0有两个不相等的实数根,
∴△=b2-4ac=4-4(1-m)>0,
即m>0,
∵另一个关于x的方程x2-(m-2)x+1-2m=0,
△=b2-4ac=(m-2)2-4(1-2m)=m2+8m=m(m+8),
又∵m>0,
∴m+8>0,
∴△=b2-4ac=m(m+8)>0,
∴此方程有两个不相等的实数根.
∴(x-1)2=m,
∵m是一个大于5而小于10的整数,且方程的两个根都是有理数,
∴m=9,
∴x-1=±3,
解得:x1=4,x2=-2,
故m的值为9和它的另一个根为2或4;
(2)∵方程x2-2x-m+1=0有两个不相等的实数根,
∴△=b2-4ac=4-4(1-m)>0,
即m>0,
∵另一个关于x的方程x2-(m-2)x+1-2m=0,
△=b2-4ac=(m-2)2-4(1-2m)=m2+8m=m(m+8),
又∵m>0,
∴m+8>0,
∴△=b2-4ac=m(m+8)>0,
∴此方程有两个不相等的实数根.
点评:此题主要考查了一元二次方程的整数根,正确掌握根的判别式是解题关键.

练习册系列答案
相关题目
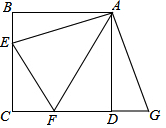 如图,正方形ABCD中,点E、F分别在边BC、CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG,求证:EF=FG.
如图,正方形ABCD中,点E、F分别在边BC、CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG,求证:EF=FG.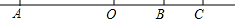 如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒)
如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒) 如图,两个三角形摆成如图所示的形状,其中EC⊥BC于点C,点D在AC边上,DE∥BC,若∠1=155°,则∠2的度数为
如图,两个三角形摆成如图所示的形状,其中EC⊥BC于点C,点D在AC边上,DE∥BC,若∠1=155°,则∠2的度数为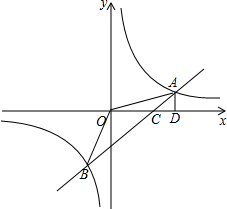 如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.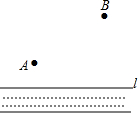 如图所示,有A、B两个村庄,A村距河边100m,B村距河边300m,两村平行于河边方向的水平距离为300m,现要在河边建一抽水站,铺设管道抽水到A村和B村,若铺设管道每米需要500元,则最低费用为多少?请画图,并解答.
如图所示,有A、B两个村庄,A村距河边100m,B村距河边300m,两村平行于河边方向的水平距离为300m,现要在河边建一抽水站,铺设管道抽水到A村和B村,若铺设管道每米需要500元,则最低费用为多少?请画图,并解答.