题目内容
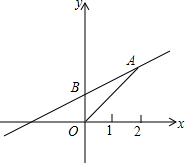 如图,已知平面直角坐标系xOy,直线y=
如图,已知平面直角坐标系xOy,直线y=| 1 |
| 2 |
| 1 |
| 2 |
(1)求b的值;
(2)如果反比例函数y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先将x=0代入y=
x+b,求出y的值,得到B(0,b),再由△AOB的面积等于1,得到
×b×2=1,解方程求出b=1;
(2)先由点A(2,t)在直线y=
x+1上,求出t=
×2+1=2,得到点A(2,2),再把A点坐标代入y=
,利用待定系数法即可求出反比例函数的解析式.
| 1 |
| 2 |
| 1 |
| 2 |
(2)先由点A(2,t)在直线y=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
解答:解:(1)∵直线y=
x+b经过第一、二、三象限,与y轴交于点B,
∴B(0,b),b>0.
∵△AOB的面积等于1,点A(2,t),
∴
×b×2=1,
∴b=1;
(2)∵点A(2,t)在直线y=
x+1上,
∴t=
×2+1=2,
∴点A(2,2).
∵反比例函数y=
的图象经过点A,
∴k=2×2=4,
∴反比例函数的解析式为y=
.
| 1 |
| 2 |
∴B(0,b),b>0.
∵△AOB的面积等于1,点A(2,t),
∴
| 1 |
| 2 |
∴b=1;
(2)∵点A(2,t)在直线y=
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
∴点A(2,2).
∵反比例函数y=
| k |
| x |
∴k=2×2=4,
∴反比例函数的解析式为y=
| 4 |
| x |
点评:本题考查了反比例函数与一次函数的交点问题,一次函数图象上点的坐标特征,三角形的面积,待定系数法求函数的解析式,难度适中.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
计算4x2•x3的结果是( )
| A、4x6 |
| B、4x5 |
| C、x6 |
| D、x5 |
将抛物线y=2(x+4)2-3的对称轴是( )
| A、直线x=4 |
| B、直线x=-4 |
| C、直线x=3 |
| D、直线x=-3 |
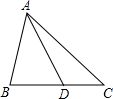 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A、AB2=BD•BC |
| B、AB2=BD•AC |
| C、AB•AD=BD•BC |
| D、AD•BC=BD•AC |
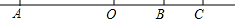 如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒)
如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒)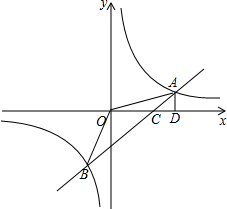 如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
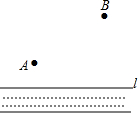 如图所示,有A、B两个村庄,A村距河边100m,B村距河边300m,两村平行于河边方向的水平距离为300m,现要在河边建一抽水站,铺设管道抽水到A村和B村,若铺设管道每米需要500元,则最低费用为多少?请画图,并解答.
如图所示,有A、B两个村庄,A村距河边100m,B村距河边300m,两村平行于河边方向的水平距离为300m,现要在河边建一抽水站,铺设管道抽水到A村和B村,若铺设管道每米需要500元,则最低费用为多少?请画图,并解答.