题目内容
抛物线y=2x2+bx+c的顶点坐标是(-1,-2),则b、c的值分别是( )
| A、-1,-2 | B、4,-2 |
| C、-4,0 | D、4,0 |
考点:二次函数的性质
专题:
分析:写出二次函数的顶点式解析式,然后展开再根据对应项系数相等解答即可.
解答:解:∵抛物线y=2x2+bx+c的顶点坐标是(-1,-2),
∴抛物线解析式为y=2(x+1)2-2=2x2+4x+2-2=2x2+4x,
∴b=4,c=0.
故选D.
∴抛物线解析式为y=2(x+1)2-2=2x2+4x+2-2=2x2+4x,
∴b=4,c=0.
故选D.
点评:本题考查了二次函数的性质,利用顶点坐标和二次项系数写出函数解析式求解更简便.

练习册系列答案
相关题目
将抛物线y=2(x+4)2-3的对称轴是( )
| A、直线x=4 |
| B、直线x=-4 |
| C、直线x=3 |
| D、直线x=-3 |
一个正方形和一个长方形的周长和为22厘米,其中正方形的边长为a厘米,长方形的一边为2a厘米,则这两个图形面积的和S与a之间的函数表达式为( )
| A、S=-3a2+11a |
| B、S=-4a2+11a |
| C、S=-9a2+22a |
| D、S=-7a2+22a |
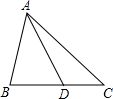 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A、AB2=BD•BC |
| B、AB2=BD•AC |
| C、AB•AD=BD•BC |
| D、AD•BC=BD•AC |
把方程-2x2-4x+1=0化为(x+h)2+k=0的形式,正确的是( )
| A、-(x+1)2-1=0 | ||
| B、(x-1)2-1=0 | ||
C、(x+1)2-
| ||
D、(2x+1)2-
|
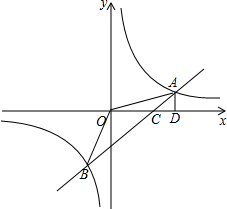 如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.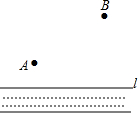 如图所示,有A、B两个村庄,A村距河边100m,B村距河边300m,两村平行于河边方向的水平距离为300m,现要在河边建一抽水站,铺设管道抽水到A村和B村,若铺设管道每米需要500元,则最低费用为多少?请画图,并解答.
如图所示,有A、B两个村庄,A村距河边100m,B村距河边300m,两村平行于河边方向的水平距离为300m,现要在河边建一抽水站,铺设管道抽水到A村和B村,若铺设管道每米需要500元,则最低费用为多少?请画图,并解答.