题目内容
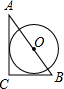 已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )
已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:切线的性质
专题:
分析:设AC,BC边上的切点D,E,连接点OC,根据切线的性质可以得到:OD⊥AC,OE⊥AC,根据三角形的面积公式,以及△ABC的面积=△AOC的面积+△BOC的面积,即可求解.
解答:解:设AC,BC边上的切点D,E,连接点OC,OD⊥AC,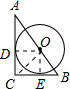 OE⊥BC,
OE⊥BC,
∵⊙O与直角边AC、BC都相切,
∴OD⊥AC,OE⊥BC,
∴S△AOC=
AC•DO,S△BOC=
BC•OE,
又∵△ABC的面积=△AOC的面积+△BOC的面积,
∴
ab=
br+
ar,
∴r=
,
故选C.
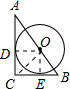 OE⊥BC,
OE⊥BC,∵⊙O与直角边AC、BC都相切,
∴OD⊥AC,OE⊥BC,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵△ABC的面积=△AOC的面积+△BOC的面积,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| ab |
| a+b |
故选C.
点评:本题主要考查了切线的性质,把求圆的半径的问题转化为三角形的面积的问题是解决本题的关键.

练习册系列答案
相关题目
 如图,数轴上的点A表示的数为a,则
如图,数轴上的点A表示的数为a,则| 1 |
| a |
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
 长为于12,宽为a的矩形纸片(6<a<12),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第1次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称第2次操作);若在第三次操作后,剩下的矩形为正方形,则a的值为
长为于12,宽为a的矩形纸片(6<a<12),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第1次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称第2次操作);若在第三次操作后,剩下的矩形为正方形,则a的值为 在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.
在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.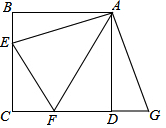 如图,正方形ABCD中,点E、F分别在边BC、CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG,求证:EF=FG.
如图,正方形ABCD中,点E、F分别在边BC、CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG,求证:EF=FG. 如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒)
如图所示,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度/秒,点B和点C运动的速度都是3个单位长度/秒,设三个点运动的时间为t(秒)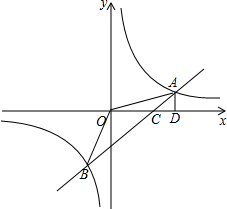 如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.
如图,一次函数的y=kx+b图象交反比例函数图象于A、B两点,交x轴于点C,AD⊥x轴于D,且OC=CD=2,S△OAD=4.