题目内容
3.解方程组:$\left\{\begin{array}{l}{x-2y=3}\\{{x}^{2}+xy-2{y}^{2}=0}\end{array}\right.$.分析 用代入法求解,将方程①变为x=2y+3,代入到②中解方程可得.
解答 解:解方程$\left\{\begin{array}{l}{x-2y=3}&{①}\\{{x}^{2}+xy-2{y}^{2}=0}&{②}\end{array}\right.$
由方程①,得:x=3+2y ③,
把③代入②,得:(3+2y)2+(3+2y)y-2y2=0,
整理,得:4y2+15y+9=0
解得:${y_1}=-\frac{3}{4}$,y2=-3
把${y_1}=-\frac{3}{4}$代入③得:${x_1}=\frac{3}{2}$,
把y2=-3代入③,得:x2=-3.
故原方程组的解是:$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{3}{4}}\end{array}\right.$,$\left\{\begin{array}{l}{x=-3}\\{y=-3}\end{array}\right.$.
点评 本题主要考查解高次方程的能力,用代入法把二元二次方程组转成一元二次方程来解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.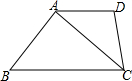 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )| A. | 9$\sqrt{7}$ | B. | 12 | C. | 8 | D. | 8$\sqrt{3}$ |
15.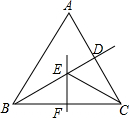 如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
 如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )| A. | 24° | B. | 30° | C. | 32° | D. | 36° |
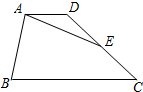 如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
 如图,已知∠2+∠3=180°,∠3=∠4=45°,则∠1的度数为45°.
如图,已知∠2+∠3=180°,∠3=∠4=45°,则∠1的度数为45°.