题目内容
11.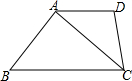 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )| A. | 9$\sqrt{7}$ | B. | 12 | C. | 8 | D. | 8$\sqrt{3}$ |
分析 根据角平分线的定义可得∠1=∠2,根据两直线平行,内错角相等可得∠2=∠3,然后得到∠1=∠3,再根据等角对等边可得CD=AD=4,过点D作DE⊥AC于E,根据等腰三角形三线合一的性质可得AE=$\frac{1}{2}$AC,根据两组角对应相等的两个三角形相似求出△ABC∽△EDC,再根据相似三角形对应边成比例求出BC,然后利用勾股定理求出AC,从而得出DE的长,最后根据四边形的面积=S△ABC+S△ADC,即可得出答案.
解答 解:∵CA是∠BCD的平分线,
∴∠1=∠2,
∵AD∥BC,
∴∠2=∠3,
∴∠1=∠3,
∵AD=4,
∴CD=AD=4,
过点D作DE⊥AC于E,则AE=CE=$\frac{1}{2}$AC,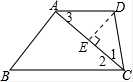 ∵∠1=∠2,∠BAC=∠DEC,
∵∠1=∠2,∠BAC=∠DEC,
∴△ABC∽△EDC,
∴$\frac{CD}{BC}$=$\frac{CE}{AC}$,
即 $\frac{4}{BC}$=$\frac{1}{2}$,
∴BC=8,
在Rt△ABC中,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{{4}^{2}-{\sqrt{7}}^{2}}$=3,
∴四边形的面积为:$\frac{1}{2}$AB•AC+$\frac{1}{2}$AC•DE=$\frac{1}{2}$×6×2$\sqrt{7}$+$\frac{1}{2}$×2$\sqrt{7}$×3=9$\sqrt{7}$.
故选A.
点评 本题考查了相似三角形的判定与性质,平行线的性质,等腰三角形三线合一的性质,勾股定理、三角形的面积公式等知识点,作辅助线构造出相似三角形并求出BC的长是解题的关键.

| A. | 直角 | B. | 钝角 | ||
| C. | 锐角 | D. | 以上三种情况都有可能 |
 如图,延长?ABCD的边AB到点E,使BE=BC,延长CD到点F,使DF=DA,连结AF,CE,求证:四边形AECF是平行四边形.
如图,延长?ABCD的边AB到点E,使BE=BC,延长CD到点F,使DF=DA,连结AF,CE,求证:四边形AECF是平行四边形. 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图: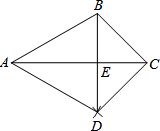 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图:
 如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可
如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可