题目内容
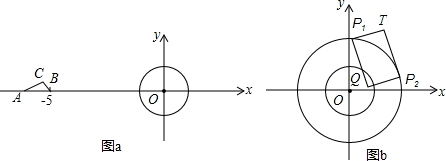
7.如图a,在平面直角坐标系xOy中,半径为1的⊙O1的圆心为坐标原点,一块直角三角板ABC的斜边AB在x轴上,A(-6,0),B(-5,0),∠BAC=30°,该三角板沿x轴正方向以每秒1个长度单位的速度运动,设运动时间为t(1)当AC边所在直线与⊙O1相切时,求t的值;
(2)当顶点C恰好在⊙O1上时,求t的值;
(3)如图b,⊙O2的圆心为坐标原点,半径为$\frac{1}{2}$,点T是第一象限内的动点,以T为顶点作矩形TP1QP2,使得点P1、P2在⊙O1上,点Q在⊙O2的内部,直接写出线段OT的取值范围.
分析 (1)画出图形求出点A运动的路程即可(注意两解).
(2)有两种情形,画出图形求出点A运动的路程即可.
(3)如图4中,当P1Q与⊙O2相切于点Q时,连接OP1,求出OT,如图5中,当Q与O重合时,四边形OP2TP1是正方形,求出此时是OT,由此即可解决问题.
解答 解:(1)如图1中,直线AC与⊙O相切于点T,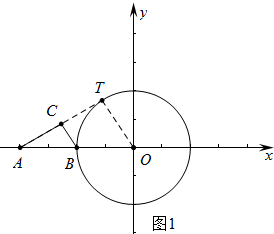
在RT△AOT中,∵∠ATO=90°,OT=1,∠TAO=30°,
∴AO=2OT=2,
∴t=6-2=4秒,
根据对称性可知,t=8时,AC边所在直线与⊙O1,
综上所述,当AC边所在直线与⊙O1相切时,t的值为2s或8s;
(2)①如图2中,连接CO,作CM⊥OA垂足为M.
∵在RT△ABC中,AB=1,∠CAB=30°,
∴BC=$\frac{1}{2}$,AC=$\frac{\sqrt{3}}{2}$,
∵$\frac{1}{2}$•AB•CM=$\frac{1}{2}$•AC•CB,
∴CM=$\frac{AC•BC}{AB}$=$\frac{\sqrt{3}}{4}$,AM=$\frac{3}{4}$,
在RT△COM中,OM=$\sqrt{O{C}^{2}-C{M}^{2}}$=$\sqrt{{1}^{2}-(\frac{\sqrt{3}}{4})^{2}}$=$\frac{\sqrt{13}}{4}$,
∴AO=AM+OM=$\frac{3}{4}$+$\frac{\sqrt{13}}{4}$,
∴t=6-($\frac{3}{4}$+$\frac{\sqrt{13}}{4}$)=$\frac{21-\sqrt{13}}{4}$.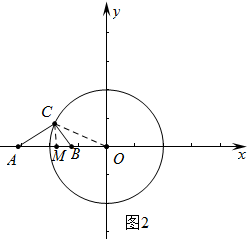
②如图3中,由①可知,OA=OM-AM=$\frac{\sqrt{13}}{4}$-$\frac{3}{4}$,
∴t=6+($\frac{\sqrt{13}}{4}$-$\frac{3}{4}$).$\frac{21+\sqrt{13}}{4}$
综上所述t=$\frac{21±\sqrt{13}}{4}$时,点C在⊙上.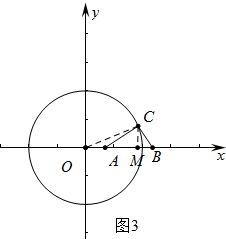
(3)如图4中,当P1Q与⊙O2相切于点Q时,连接OP1,
∵∠OQP1=∠OP2T=90°,
∴O、Q、P2共线,
在RT△OQP1中,QP1=$\sqrt{O{{P}_{1}}^{2}-O{Q}^{2}}$=$\frac{\sqrt{3}}{2}$,
∵四边形TP1QP2是矩形,
∴P2T=P1Q=$\frac{\sqrt{3}}{2}$,
在RT△OP2T中,OT=$\sqrt{O{{P}_{2}}^{2}+{P}_{2}{T}^{2}}$=$\frac{\sqrt{7}}{2}$,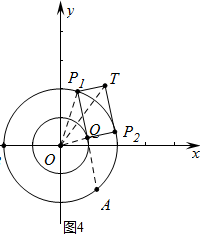
如图5中,当Q与O重合时,四边形OP2TP1是正方形,此时OT=$\sqrt{2}$,
综上所述,当点Q在⊙O2的内部时,$\frac{\sqrt{7}}{2}$<OT≤$\sqrt{2}$.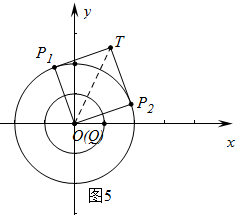
点评 本题考查圆的有关性质、勾股定理等知识,解题的关键是正确画出图形,第三个问题需要找到两个特殊位置确定OT的取值范围,注意点Q在⊙O2内部这个条件,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | $\sqrt{8}-\sqrt{3}=\sqrt{8-3}$ | B. | 2$+\sqrt{3}=2\sqrt{3}$ | C. | $\sqrt{2}(\sqrt{3}+1)=\sqrt{6}+1$ | D. | 3$\sqrt{2}-2\sqrt{2}=\sqrt{2}$ |
| A. | 2 | B. | 1 | C. | 3 | D. | 4 |
| A. | 直角 | B. | 钝角 | ||
| C. | 锐角 | D. | 以上三种情况都有可能 |
 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图: 如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可
如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可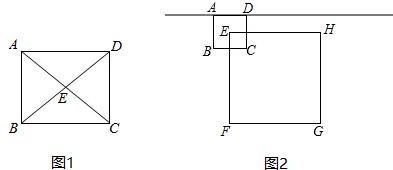
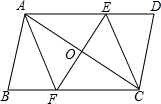 已知:如图,在?ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
已知:如图,在?ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.