题目内容
8.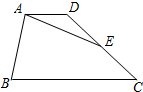 如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
分析 首先连接AC,由在梯形ABCD中,AD∥BC,且BC=3AD,可求得$\overrightarrow{BC}$,然后由三角形法则求得$\overrightarrow{AC}$,继而求得$\overrightarrow{DC}$,然后由点E是边DC的中点,求得$\overrightarrow{DE}$,继而求得答案.
解答 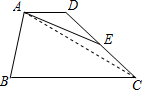 解:连接AC,
解:连接AC,
∵在梯形ABCD中,AD∥BC,且BC=3AD,
∴$\overrightarrow{BC}$=3$\overrightarrow{AD}$=3$\overrightarrow{b}$,
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{a}$+3$\overrightarrow{b}$,
∴$\overrightarrow{DC}$=$\overrightarrow{AC}$-$\overrightarrow{AD}$=($\overrightarrow{a}$+3$\overrightarrow{b}$)-$\overrightarrow{b}$=$\overrightarrow{a}$+2$\overrightarrow{b}$,
∵点E是边DC的中点,
∴$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=$\overrightarrow{b}$+($\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$.
故答案为:$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$.
点评 此题考查了平面向量的知以及梯形的性质.注意掌握三角形法则的应用是解此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案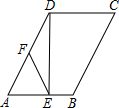 如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
| A. | $\sqrt{8}-\sqrt{3}=\sqrt{8-3}$ | B. | 2$+\sqrt{3}=2\sqrt{3}$ | C. | $\sqrt{2}(\sqrt{3}+1)=\sqrt{6}+1$ | D. | 3$\sqrt{2}-2\sqrt{2}=\sqrt{2}$ |
 星期天墨墨在家玩俄罗斯方块,遇到如图所示的情形,他要将“T”方块A放到B位置,需将“T”方块A( )
星期天墨墨在家玩俄罗斯方块,遇到如图所示的情形,他要将“T”方块A放到B位置,需将“T”方块A( )| A. | 先向右平移1个小格,再向下平移3个小格 | |
| B. | 先向右平移2个小格,再向下平移3个小格 | |
| C. | 先向右平移1个小格,再向下平移4个小格 | |
| D. | 先向右平移2个小格,再向下平移4个小格 |
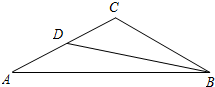 如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求:
如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求: 如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可
如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件AC=BD或∠ABC=90°,可