题目内容
17.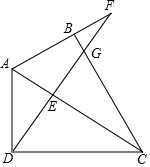 如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.
分析 利用相似三角形的判定方法得出△ADE∽△ACD,△AEF∽△ABC,进而求出AD2=AB•AF.
解答 证明:
∵∠ADC=90°,DF⊥AC于E,
∴△ADE∽△ACD,
∴$\frac{AD}{AC}=\frac{AE}{AD}$,
∴AD2=AC•AE,
∵∠ABC=∠ADC=90°,DF⊥AC于E,
∴∠AEF=∠ABC=90°,
∴∠BFG+∠BGF=∠EGC+∠ECG=90°,
∵∠BGF=∠EGC,
∴∠BFG=∠ECG,
∴△AEF∽△ABC,
∴$\frac{AF}{AC}=\frac{AE}{AB}$,
∴AC•AE=AB•AF,
∴AD2=AB•AF.
点评 此题主要考查了相似三角形的判定与性质,得出△ADE∽△ACD,△AEF∽△ABC是证题关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12. 如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
 如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )| A. | $\sqrt{2}-3$ | B. | 2$\sqrt{2}$-1 | C. | 3$\sqrt{2}$-3 | D. | 2-$\sqrt{2}$ |
 如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.
如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.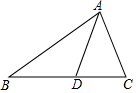 如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.
如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.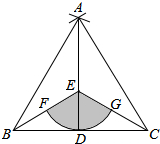 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.  如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.