题目内容
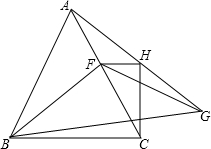 已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.
已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.考点:相似形综合题
专题:
分析:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,设AB=BC=AC=a,BF=b,根据AM⊥BC,FR⊥BC,GN⊥BC,得出AM∥FR∥GN,求出∠CBQ=∠FBG,从而得出∠FBQ=∠GBM,求出BQ=
a,再根据相似三角形的性质得出BN的值,再根据直角三角形的性质,得出FR=CH,最后根据FR∥CH,CH⊥BC,得出四边形CHFR是矩形,从而得出答案.
| ||
| 2 |
解答: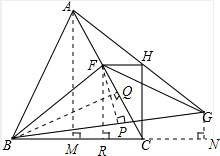 解:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,
解:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,
设AB=BC=AC=a,BF=b,
∵AM⊥BC,FR⊥BC,GN⊥BC,
∴AM∥FR∥GN,∠CBQ=∠FBG=30°,
∴∠FBQ=∠GBM,BQ=
a,
∵△BGF是等腰三角形,∠FBG=30°,
∴BG=2BP=
b,
可证△BGN∽△BQF,
∴
=
=
,
即
=
,
∴BN=
a,
∴CN=BN-BC=
a=CM,
∴CH是梯形AMNG的中位线,
∴CH=
(GN+AM),
∵QF=
=
=
,
∴GN=
=
=
,
∵AM=
a,
∴CH=
(
a+
)=
(a+
),
CF=CQ+QF=
a+
,
∴FR=
CF=
(a+
)=CH,
∵FR∥CH,CH⊥BC,
∴四边形CHFR是矩形,
∴FH⊥CH.
 解:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,
解:作AM⊥BC,BQ⊥AC,FP⊥BQ,FR⊥BC,GN⊥BC延长线于N,设AB=BC=AC=a,BF=b,
∵AM⊥BC,FR⊥BC,GN⊥BC,
∴AM∥FR∥GN,∠CBQ=∠FBG=30°,
∴∠FBQ=∠GBM,BQ=
| ||
| 2 |
∵△BGF是等腰三角形,∠FBG=30°,
∴BG=2BP=
| 3 |
可证△BGN∽△BQF,
∴
| BQ |
| BN |
| BF |
| BG |
| QF |
| GN |
即
| ||||
| BN |
| b | ||
|
∴BN=
| 3 |
| 2 |
∴CN=BN-BC=
| 1 |
| 2 |
∴CH是梯形AMNG的中位线,
∴CH=
| 1 |
| 2 |
∵QF=
| BF2-BQ2 |
b2-
|
| 1 |
| 2 |
| 4b2-3a2 |
∴GN=
| QF•BG |
| BF |
| ||||||
| b |
| ||
| 2 |
| 4b2-3a2 |
∵AM=
| ||
| 2 |
∴CH=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 4b2-3a2 |
| ||
| 4 |
| 4b2-3a2 |
CF=CQ+QF=
| 1 |
| 2 |
| 1 |
| 2 |
| b2-3a2 |
∴FR=
| ||
| 2 |
| ||
| 4 |
| 4b2-3a2 |
∵FR∥CH,CH⊥BC,
∴四边形CHFR是矩形,
∴FH⊥CH.
点评:此题考查了相似形的综合,用到的知识点是相似三角形的判定与性质、矩形的性质、直角三角形的性质等知识点,熟练掌握性质定理是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
若A=10a2+2b2-7a+6,B=a2+2b2+5a-1,则A-B的值是( )
| A、正数 | B、负数 | C、0 | D、可正可负 |
 一个上底和下底都是等边三角形的盒子,等边三角形的高为70cm,盒子的高为240cm,M为AB的中点,在M处有一只飞蛾要飞到E处,它的最短行程多少?
一个上底和下底都是等边三角形的盒子,等边三角形的高为70cm,盒子的高为240cm,M为AB的中点,在M处有一只飞蛾要飞到E处,它的最短行程多少?
 如图,已知△ABC≌△DEC,B、C、D三点在同一直线上,∠B=60°,求∠1的度数.
如图,已知△ABC≌△DEC,B、C、D三点在同一直线上,∠B=60°,求∠1的度数.