题目内容
如图,△ABC中,AB=AC,∠ABC的角平分线交AC于N,NM∥BC,NH⊥BC于H,P在直线MN上,过点P作边AB、AC的垂线分别为E、F.
(1)如图1,当点P在线段MN上时,判断PE、PF、NH之间的数量关系,并证明.
(2)如图2,当点P在线段MN的延长线上时,则PE、PF、NH之间的数量关系为
(3)如图3,在(2)条件下,当∠A=36°,PE=6,△APN的面积等于△NBC的面积时,求PF的长?
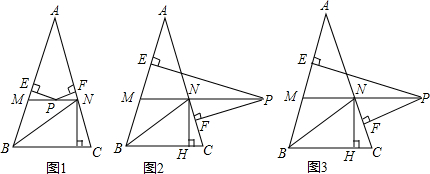
(1)如图1,当点P在线段MN上时,判断PE、PF、NH之间的数量关系,并证明.
(2)如图2,当点P在线段MN的延长线上时,则PE、PF、NH之间的数量关系为
(3)如图3,在(2)条件下,当∠A=36°,PE=6,△APN的面积等于△NBC的面积时,求PF的长?

考点:全等三角形的判定与性质,角平分线的性质,等腰三角形的性质
专题:解题思想
分析:(1)PE+PF=NH,过点N作DN⊥AB,垂足为D,过点P作PG⊥DN,垂足为G,则四边形EPGD是矩形,得到PE=DG,然后证明△PGN≌△NFP(AAS),得到PF=GN,由角平分线的性质,得到DN=NH,从而得到结论:PE+PF=NH.
(2)PE=PF+NH,基本思路同(1).
(3)由(2)可知∠4=∠5=∠6,∵∠A=36°,AB=AC,可得AN=BN=BC,由△APN的面积等于△NBC的面积,可得AN•PF=BC•NH,∴PF=NH,进而得到PF=3.
(2)PE=PF+NH,基本思路同(1).
(3)由(2)可知∠4=∠5=∠6,∵∠A=36°,AB=AC,可得AN=BN=BC,由△APN的面积等于△NBC的面积,可得AN•PF=BC•NH,∴PF=NH,进而得到PF=3.
解答:(1)PE+PF=NH,
证明:过点N作DN⊥AB,垂足为D,过点P作PG⊥DN,垂足为G,
则四边形EPGD是矩形,
∴PE=DG,
∵PG⊥DN,BD⊥DN,
∴PG∥DM,
∴∠AMN=∠GPN,
∵AB=AC,
∴∠ABC=∠C,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠C,
∴∠AMN=∠ANM,
∴∠GPN=∠FNP.
∵∠PGN=∠NFP=90°,PN=PN,
∴△PGN≌△NFP(AAS),
∴PF=GN,
∴EP+FP=DG+GN=DN,
∵BN平分∠ABC,ND⊥AB,NH⊥BC,
∴DN=NH,
即:PE+PF=NH.
(2)PE=PF+NH,
理由如下:
过点N分别作ND⊥AB,垂足为D,NG⊥EP,垂足为G,
则四边形DNGE是矩形,
∴DN=EG,DN∥EP,
∴∠1=∠3,
∵BN平分∠ABC,MN∥BC,
∴∠5=∠6=∠4,
∴BM=MN,
∵BM=NC,
∴MN=NC,
∵DN=NH,
∴Rt△MND≌Rt△CNH(HL),
∴∠1=∠2,
∴∠2=∠3,
∵MN∥BC,NH⊥BC,
∴NH⊥MN,
∴∠2+∠7=90°
∵∠3+∠GNP=90°,
∴∠7=∠GNP,
∵∠NGP=∠NFP=90°,NP=NP,
∴△PGN≌△PFN(AAS),
∴PF=PG,
∵DN=NH,
∴PF+NH=PG+DN=PG+EG=EP,
即:EP=PF+NH.
(3)解:由(2)可知∠4=∠5=∠6,
∵∠A=36°,AB=AC,
∴∠4=∠5=∠6=∠A=36°,∠C=∠BNC=72°,
∴AN=BN=BC,
∵△APN的面积等于△NBC的面积,
∴AN•PF=BC•NH,
∴PF=NH,
∵EP=PF+NH,PE=6,
∴PF=3.

证明:过点N作DN⊥AB,垂足为D,过点P作PG⊥DN,垂足为G,
则四边形EPGD是矩形,
∴PE=DG,
∵PG⊥DN,BD⊥DN,
∴PG∥DM,
∴∠AMN=∠GPN,
∵AB=AC,
∴∠ABC=∠C,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠C,
∴∠AMN=∠ANM,
∴∠GPN=∠FNP.
∵∠PGN=∠NFP=90°,PN=PN,
∴△PGN≌△NFP(AAS),
∴PF=GN,
∴EP+FP=DG+GN=DN,
∵BN平分∠ABC,ND⊥AB,NH⊥BC,
∴DN=NH,
即:PE+PF=NH.
(2)PE=PF+NH,
理由如下:
过点N分别作ND⊥AB,垂足为D,NG⊥EP,垂足为G,
则四边形DNGE是矩形,
∴DN=EG,DN∥EP,
∴∠1=∠3,
∵BN平分∠ABC,MN∥BC,
∴∠5=∠6=∠4,
∴BM=MN,
∵BM=NC,
∴MN=NC,
∵DN=NH,
∴Rt△MND≌Rt△CNH(HL),
∴∠1=∠2,
∴∠2=∠3,
∵MN∥BC,NH⊥BC,
∴NH⊥MN,
∴∠2+∠7=90°
∵∠3+∠GNP=90°,
∴∠7=∠GNP,
∵∠NGP=∠NFP=90°,NP=NP,
∴△PGN≌△PFN(AAS),
∴PF=PG,
∵DN=NH,
∴PF+NH=PG+DN=PG+EG=EP,
即:EP=PF+NH.
(3)解:由(2)可知∠4=∠5=∠6,
∵∠A=36°,AB=AC,
∴∠4=∠5=∠6=∠A=36°,∠C=∠BNC=72°,
∴AN=BN=BC,
∵△APN的面积等于△NBC的面积,
∴AN•PF=BC•NH,
∴PF=NH,
∵EP=PF+NH,PE=6,
∴PF=3.

点评:此题主要考查了全等三角形的判定与性质,等腰三角形的性质,解决的此题基本思想是“截长法”,证明两条短线段之和等于长线段.

练习册系列答案
相关题目
 如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF=( )
如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF=( )| A、60° | B、30° |
| C、60° | D、75° |
 △ABC内接于⊙O且AB>AC,直径PD⊥BC,过P作PE⊥AB于E,PF⊥CA的延长线于F,求证:AE=
△ABC内接于⊙O且AB>AC,直径PD⊥BC,过P作PE⊥AB于E,PF⊥CA的延长线于F,求证:AE= 已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.
已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC. 用若干大小相同的小立方块搭一个几何体,从正面和上面看到的几何体的形状图如图所示,根据你所搭几何体画出从左面看到的它的形状图,你还能搭出满足条件的其他几何体吗?
用若干大小相同的小立方块搭一个几何体,从正面和上面看到的几何体的形状图如图所示,根据你所搭几何体画出从左面看到的它的形状图,你还能搭出满足条件的其他几何体吗? 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=22°,求∠AOB的度数.
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=22°,求∠AOB的度数.