题目内容
若A=10a2+2b2-7a+6,B=a2+2b2+5a-1,则A-B的值是( )
| A、正数 | B、负数 | C、0 | D、可正可负 |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:此题可直接用多项式M减去多项式N,然后化简,最后把得出的结果与零比较确定M-N的正负.
解答:解:A-B=10a2+2b2-7a+6-a2-2b2-5a+1
=9a2-12a+7
=9[a2-
a+(-
)2]+7-9×(-
)2
=9(a-
)2+3,
∵9(a-
)2≥0,
∴9(a-
)2+3>0,即A-B>0.
∴A-B的值是正数.
故选:A.
=9a2-12a+7
=9[a2-
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
=9(a-
| 2 |
| 3 |
∵9(a-
| 2 |
| 3 |
∴9(a-
| 2 |
| 3 |
∴A-B的值是正数.
故选:A.
点评:本题考查了整式的加减,需注意整式的加减运算;另外题中含有的配方得完全平方式的思想,同学们也需要灵活掌握.

练习册系列答案
相关题目
下列单项式中,与2x4y是同类项的为( )
| A、2x4 |
| B、2xy |
| C、-2x2y3 |
| D、x4y |
下列结论中正确的个数( )
①甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地方比最低的地方高35米;
②|3.14-π|=0;
③-|-
|的相反数是-
;
④最小的正整数是1;
⑤最大的负整数为-1;
⑥绝对值最小的有理数为0.
①甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地方比最低的地方高35米;
②|3.14-π|=0;
③-|-
| 2 |
| 3 |
| 2 |
| 3 |
④最小的正整数是1;
⑤最大的负整数为-1;
⑥绝对值最小的有理数为0.
| A、3个 | B、4个 | C、5个 | D、6个 |
已知直线y=kx+b过点A(x1,y1)和点B(x2,y2),若k<0,x1<x2,则y1与y2的大小关系为( )
| A、y1<y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、不能确定 |
 如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF=( )
如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF=( )| A、60° | B、30° |
| C、60° | D、75° |
关于函数y=x+1,下列结论正确的是( )
| A、图象必经过点(-2,1) |
| B、y随x的增大减小 |
| C、当x>-1时,y<0 |
| D、图象经过第一、二、三象限 |
 如图,在直角梯形ABCD中,AD∥BC且AD=
如图,在直角梯形ABCD中,AD∥BC且AD=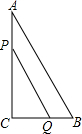 如图,在Rt△ACB中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动,它们的速度都是1米/秒,问:几秒后△PCQ的面积为Rt△ACB面积的一半?
如图,在Rt△ACB中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动,它们的速度都是1米/秒,问:几秒后△PCQ的面积为Rt△ACB面积的一半?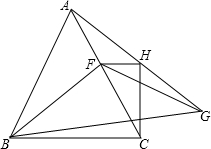 已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.
已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.