题目内容
一个上底和下底都是等边三角形的盒子，等边三角形的高为70cm，盒子的高为240cm，M为AB的中点，在M处有一只飞蛾要飞到E处，它的最短行程多少？考点：平面展开-最短路径问题
专题：
分析：根据题意得出ME2=702+2402=62500，进而求出即可．
解答：
解：连接MC，ME，
得MC⊥EC，即△MEC是直角三角形，
由勾股定理，得ME2=702+2402=62500，
解得：ME=250
故在M处有一只飞蛾要飞到E处，它的最短行程为250cm．
解：连接MC，ME，得MC⊥EC，即△MEC是直角三角形，
由勾股定理，得ME2=702+2402=62500，
解得：ME=250
故在M处有一只飞蛾要飞到E处，它的最短行程为250cm．
点评：此题主要考查了平面展开图最短路径问题，得出△MEC是直角三角形是解题关键．
练习册系列答案
相关题目
已知直线y=kx+b过点A（x1，y1）和点B（x2，y2），若k＜0，x1＜x2，则y1与y2的大小关系为（ ）
| A、y1＜y2 |
| B、y1=y2 |
| C、y1＞y2 |
| D、不能确定 |
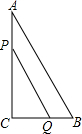如图，在Rt△ACB中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动，它们的速度都是1米/秒，问：几秒后△PCQ的面积为Rt△ACB面积的一半？
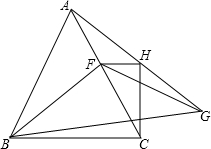已知△ABC是等边三角形，∠FBG=30°，FB=FG，CH⊥BC交AG于H，求证：FH⊥HC．