题目内容
王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)问第一条边长可以为8米吗?为什么?
(2)能围成等腰三角形吗?若能,请求出a的值;若不能,请说明理由.
(1)问第一条边长可以为8米吗?为什么?
(2)能围成等腰三角形吗?若能,请求出a的值;若不能,请说明理由.
考点:一元一次不等式组的应用,三角形三边关系
专题:
分析:(1)本题需先求出三边的长,再根据三角形的三边关系列出不等式组,即可求出a的取值范围.
(2)本题需先求出a的值,然后即可得出三角形的三边长.
(2)本题需先求出a的值,然后即可得出三角形的三边长.
解答:解:(1)∵第二条边长为2a+2,
∴第三条边长为30-a-(2a+2)
=28-3a.
当a=8时,三边长分别为8,18,4,
由于8+4<18,所以不能构成三角形,即第一条边长不能为8米;
(2)能.理由如下:
当a=2a+2时,a=-2,不合题意,不能构成等腰三角形;
当a=28-3a时,a=7,则该三角形的三边为:7,16,7,由于7+7<16,所以不能构成三角形;
当2a+2=28-3a时,a=
,则该三角形的三边为:
,
,
,由于0<
<
,所以能构成等腰三角形;
综上所述,当a=
时,能构成等腰三角形.
∴第三条边长为30-a-(2a+2)
=28-3a.
当a=8时,三边长分别为8,18,4,
由于8+4<18,所以不能构成三角形,即第一条边长不能为8米;
(2)能.理由如下:
当a=2a+2时,a=-2,不合题意,不能构成等腰三角形;
当a=28-3a时,a=7,则该三角形的三边为:7,16,7,由于7+7<16,所以不能构成三角形;
当2a+2=28-3a时,a=
| 26 |
| 5 |
| 26 |
| 5 |
| 62 |
| 5 |
| 62 |
| 5 |
| 26 |
| 5 |
| 144 |
| 5 |
综上所述,当a=
| 26 |
| 5 |
点评:本题主要考查了一元一次不等式组的应用,在解题时要能根据三角形的三边关系,列出不等式组是本题的关键.

练习册系列答案
相关题目
下列结论中正确的个数( )
①甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地方比最低的地方高35米;
②|3.14-π|=0;
③-|-
|的相反数是-
;
④最小的正整数是1;
⑤最大的负整数为-1;
⑥绝对值最小的有理数为0.
①甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地方比最低的地方高35米;
②|3.14-π|=0;
③-|-
| 2 |
| 3 |
| 2 |
| 3 |
④最小的正整数是1;
⑤最大的负整数为-1;
⑥绝对值最小的有理数为0.
| A、3个 | B、4个 | C、5个 | D、6个 |
 如图,在直角梯形ABCD中,AD∥BC且AD=
如图,在直角梯形ABCD中,AD∥BC且AD=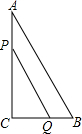 如图,在Rt△ACB中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动,它们的速度都是1米/秒,问:几秒后△PCQ的面积为Rt△ACB面积的一半?
如图,在Rt△ACB中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发分别沿AC、BC向点C匀速移动,它们的速度都是1米/秒,问:几秒后△PCQ的面积为Rt△ACB面积的一半? △ABC内接于⊙O且AB>AC,直径PD⊥BC,过P作PE⊥AB于E,PF⊥CA的延长线于F,求证:AE=
△ABC内接于⊙O且AB>AC,直径PD⊥BC,过P作PE⊥AB于E,PF⊥CA的延长线于F,求证:AE=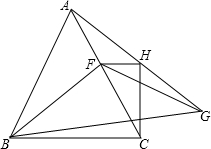 已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.
已知△ABC是等边三角形,∠FBG=30°,FB=FG,CH⊥BC交AG于H,求证:FH⊥HC.