Question

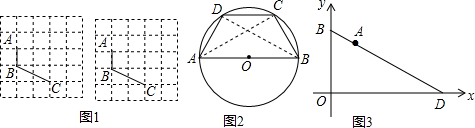
3．将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起．

（1）如图（1）若∠BOD=35°，则∠AOC=145°；若∠AOC=135°，则∠BOD=45°；
（2）如图（2）若∠AOC=140°，则∠BOD=40°；
（3）猜想∠AOC与∠BOD的大小关系，并结合图（1）说明理由．
（4）三角尺AOB不动，将三角尺COD的OD边与OA边重合，然后绕点O按顺时针或逆时针方向任意转动一个角度，当∠AOD（0°＜∠AOD＜90°）等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠AOD角度所有可能的值，不用说明理由．

Answer 1

分析 （1）由于是两直角三角形板重叠，根据∠AOC=∠AOB+∠COD-∠BOD可分别计算出∠AOC、∠BOD的度数；
（2）根据∠BOD=360°-∠AOC-∠AOB-∠COD计算可得；
（3）由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补；
（4）分别利用OD⊥AB、CD⊥OB、CD⊥AB、OC⊥AB分别求出即可．

解答 解：（1）若∠BOD=35°，∵∠AOB=∠COD=90°，
∴∠AOC=∠AOB+∠COD-∠BOD=90°+90°-35°=145°，
若∠AOC=135°，
则∠BOD=∠AOB+∠COD-∠AOC=90°+90°-135°=45°；

（2）如图2，若∠AOC=140°，
则∠BOD=360°-∠AOC-∠AOB-∠COD=40°；

（3）∠AOC与∠BOD互补．
∵∠AOD+∠BOD+∠BOD+∠BOC=180°．
∵∠AOD+∠BOD+∠BOC=∠AOC，
∴∠AOC+∠BOD=180°，
即∠AOC与∠BOD互补．

（4）OD⊥AB时，∠AOD=30°，
CD⊥OB时，∠AOD=45°，
CD⊥AB时，∠AOD=75°，
OC⊥AB时，∠AOD=60°，
即∠AOD角度所有可能的值为：30°、45°、60°、75°；
故答案为：（1）145°，45°；（2）40°．

点评 本题题主要考查了互补、互余的定义等知识，解决本题的关键是理解重叠的部分实质是两个角的重叠．