题目内容
15.定义:数学活动课上,兵兵老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.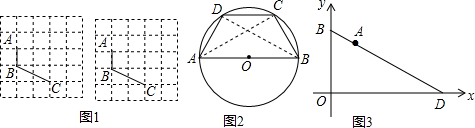
理解:
(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请用两种不同的方法再画出一个格点D,使四边形ABCD为对等四边形;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.试说明:四边形ABCD是对等四边形;
(3)如图3,点D,B分别在x轴和y轴上,且D(8,0),cos∠BDO=$\frac{4}{5}$,点A是边BD上的一点,且AD:AB=4:试在x轴上找一点C,使四边形ABOC为对等四边形,请直接写出所有满足条件的C点坐标.
分析 (1)根据对等四边形的定义画出图形即可;
(2)根据圆周角定理得到∠ADB=90°,∠ACD=90°,根据直角三角形全等的判定定理证明Rt△ADB≌Rt△BCA,根据全等三角形的性质证明即可;
(3)分OC=AB、AC=OB两种情况,根据平行线分线段成比例定理计算即可.
解答  解:(1)如图1:四边形ABCD为对等四边形;
解:(1)如图1:四边形ABCD为对等四边形;
(2)证明:∵AB是⊙O的直径,
∴∠ADB=90°,∠ACD=90°,
在Rt△ADB和Rt△BCA中,
$\left\{\begin{array}{l}{BD=AC}\\{BA=AB}\end{array}\right.$,
∴Rt△ADB≌Rt△BCA,
∴AD=BC,
∴四边形ABCD是对等四边形;
(3) ∵D(8,0),
∵D(8,0),
∴OD=8,
cos∠BDO=$\frac{4}{5}$,即$\frac{OD}{BD}$=$\frac{4}{5}$,
∴BD=10,
由勾股定理得,OB=$\sqrt{B{D}^{2}-O{D}^{2}}$=6,
∵AD:AB=4,BD=10,
∴AB=2,AD=8,
如图3,当OC=AB时,C点坐标为(2,0),
如图4,当AC=OB时,AC=6,
作AE⊥OD于E,
则AE∥OB,
∴$\frac{AE}{OB}$=$\frac{DE}{DO}$=$\frac{DA}{DB}$,即$\frac{AE}{6}$=$\frac{DE}{8}$=$\frac{8}{10}$,
解得AE=$\frac{24}{5}$,DE=$\frac{32}{5}$,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\frac{18}{5}$,
OE=OD-DE=$\frac{8}{5}$,
则OC=OE+EC=$\frac{26}{5}$,
∴C点坐标为($\frac{26}{5}$,0),
∴四边形ABOC为对等四边形时,C点坐标为:(2,0)或($\frac{26}{5}$,0).
点评 本题考查的是圆周角定理、勾股定理的应用以及平行线分线段成比例定理,正确理解对等四边形的定义、正确运用相关的定理和性质是解题的关键.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 2,3,5 | B. | 4,5,6 | C. | 11,12,15 | D. | 8,15,17 |
 如图,以Rt△ABC直角边BC为直径作⊙O,交AB边于点D,已知AC=2,∠B=30°,则阴影部分面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.
如图,以Rt△ABC直角边BC为直径作⊙O,交AB边于点D,已知AC=2,∠B=30°,则阴影部分面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.
 如图,已知△ABC和△DCE均是等边三角形,点B,C,E在同条直线上,AE与BD交于点O,AE与CD相交于点G,AC与BD交于点F,连结0C,FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOA=60°,其中正确的有( )
如图,已知△ABC和△DCE均是等边三角形,点B,C,E在同条直线上,AE与BD交于点O,AE与CD相交于点G,AC与BD交于点F,连结0C,FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOA=60°,其中正确的有( )