题目内容
多项式-6ab2+18a2b2-12a3b2c的公因式是( )
A.-6ab2c B.-ab2 C.-6ab2 D.-6a3b2c
 C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C.
C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C.
练习册系列答案
相关题目
平移前后的两个图形相互比较而言,下列说法正确的是( )
A. 两个图形大小不一样
B. 两个图形的形状不一样
C. 平移前比平移后小
D. 两个图形全等
 D
【解析】试题解析:平移不改变图形的大小和形状,平移前后的两个图形全等.
故选D.
D
【解析】试题解析:平移不改变图形的大小和形状,平移前后的两个图形全等.
故选D. 如图,在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F的度数是( )
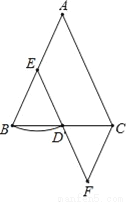
A. 40 B. 70 C. 50 D. 45
 A
【解析】【解析】
∵以点E为圆心,EB为半径画弧,交BC于点D,∴EB=ED,∴∠EDB=∠B=70°,∴∠BED=180°﹣∠B=∠BDE=40°.
∵AB=AC,∴∠ACB=∠B,∴∠EDB=∠ACB,∴EF∥AC.
∵E是AB的中点,即BE=AE,∴BD=CD.
在△EBD和△FCD中,∵DE=DF,∠EDB=∠CDF,BD=CD,∴△EBD≌△FCD(SAS)...
A
【解析】【解析】
∵以点E为圆心,EB为半径画弧,交BC于点D,∴EB=ED,∴∠EDB=∠B=70°,∴∠BED=180°﹣∠B=∠BDE=40°.
∵AB=AC,∴∠ACB=∠B,∴∠EDB=∠ACB,∴EF∥AC.
∵E是AB的中点,即BE=AE,∴BD=CD.
在△EBD和△FCD中,∵DE=DF,∠EDB=∠CDF,BD=CD,∴△EBD≌△FCD(SAS)... 将 分解因式,应提取的公因式是___________
分解因式,应提取的公因式是___________
 【解析】由x-y与y-x互为相反数,变形后提公因式3(x-y),可得=3(x-y)(a-3b).
故答案为:3(x-y).
【解析】由x-y与y-x互为相反数,变形后提公因式3(x-y),可得=3(x-y)(a-3b).
故答案为:3(x-y). 一个多项式因式分解后是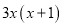 ,那么这个多项式是( )
,那么这个多项式是( )
A. 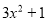 B.
B. 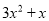 C.
C. 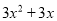 D.
D. 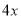
 C
【解析】利用因式分解是整式乘法的逆运算,可知=3x2+3x.
故选:C.
C
【解析】利用因式分解是整式乘法的逆运算,可知=3x2+3x.
故选:C. 如果x2+2(m-3)x+25能用公式法分解因式,那么m的值是多少?
 m=8或-2.
【解析】试题分析:利用完全平方公式的结构特征判断即可确定出m的值,注意包括两种情况.
试题解析:∵x2+2(m-3)x+25能用公式法分解因式,
∴2(m-3)=±10,
解得:m=8或-2.
m=8或-2.
【解析】试题分析:利用完全平方公式的结构特征判断即可确定出m的值,注意包括两种情况.
试题解析:∵x2+2(m-3)x+25能用公式法分解因式,
∴2(m-3)=±10,
解得:m=8或-2. 分解因式 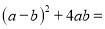 _____________
_____________
 【解析】根据完全平方公式进行相乘,合并同类项之后再利用完全平方公式因式分解为: .
故答案为: .
【解析】根据完全平方公式进行相乘,合并同类项之后再利用完全平方公式因式分解为: .
故答案为: . 如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
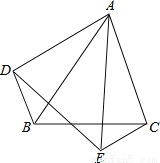
 证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等.
证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等. 在代数式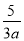 ,
, 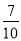 ,
, 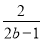 ,
, 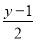 ,x+
,x+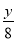 中,是分式的有( )
中,是分式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】在代数式, ,, ,x+的分母中均不含有字母,因此它们是整式,而不是分式.
而,分母中含有字母,因此是分式.
故选B.
B
【解析】在代数式, ,, ,x+的分母中均不含有字母,因此它们是整式,而不是分式.
而,分母中含有字母,因此是分式.
故选B. 
