题目内容
分解因式 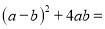 _____________
_____________
 【解析】根据完全平方公式进行相乘,合并同类项之后再利用完全平方公式因式分解为: .
故答案为: .
【解析】根据完全平方公式进行相乘,合并同类项之后再利用完全平方公式因式分解为: .
故答案为: .
练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若不等式ax-2>0的解集为x<-2,求关于y的方程ay+2=0的解
 2
【解析】试题分析:根据不等式ax-2>0的解集为x<-2即可确定a的值,然后代入方程,解方程求得.
试题解析:∵不等式ax-2>0,即ax>2的解集为x<-2,
∴a=-1,
代入方程得:-y+2=0,
解得:y=2.
2
【解析】试题分析:根据不等式ax-2>0的解集为x<-2即可确定a的值,然后代入方程,解方程求得.
试题解析:∵不等式ax-2>0,即ax>2的解集为x<-2,
∴a=-1,
代入方程得:-y+2=0,
解得:y=2. 分解因式: 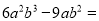 _______
_______
 【解析】根据提公因式法分解因式,可得=.
故答案为: .
【解析】根据提公因式法分解因式,可得=.
故答案为: . 多项式-6ab2+18a2b2-12a3b2c的公因式是( )
A.-6ab2c B.-ab2 C.-6ab2 D.-6a3b2c
 C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C.
C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C. 分解因式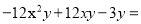 ___________
___________
 【解析】根据因式分解的方法,先提公因式-3y,再根据完全平方公式分解因式为: .
故答案为: .
【解析】根据因式分解的方法,先提公因式-3y,再根据完全平方公式分解因式为: .
故答案为: . 下列式子分解因式能用公式法分解因式的是 ( ).
A. 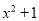 B.
B. 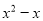 C.
C. 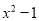 D.
D. 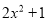
 C
【解析】根据平方差公式: ,可知因式分解为: .
故选:C.
C
【解析】根据平方差公式: ,可知因式分解为: .
故选:C. 下列多项式,能用公式法分解因式的有( )
①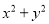 ②
②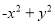 ③
③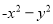 ④
④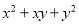
⑤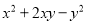 ⑥
⑥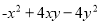
A. 2个 B. 3个 C. 4个 D. 5个
 A
【解析】根据完全平方公式,平方差公式,
的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A.
A
【解析】根据完全平方公式,平方差公式,
的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A. 使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
 D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错...
D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错... 若x>y,则下列式子中错误的是( )
A. x-3>y-3 B. x+3>y+3
C. -3x>-3y D. 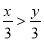
 C
【解析】试题分析:A、不等式的两边都减3,不等号的方向不变,故A正确;
B、不等式的两边都加3,不等号方向不变,故B正确;
C、不等式的两边都乘-3,不等号的方向改变,故C错误;
D、不等式的两边都除以3,不等号的方向改变,故D正确;
故选C.
C
【解析】试题分析:A、不等式的两边都减3,不等号的方向不变,故A正确;
B、不等式的两边都加3,不等号方向不变,故B正确;
C、不等式的两边都乘-3,不等号的方向改变,故C错误;
D、不等式的两边都除以3,不等号的方向改变,故D正确;
故选C. 
