题目内容
一个多项式因式分解后是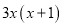 ,那么这个多项式是( )
,那么这个多项式是( )
A. 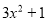 B.
B. 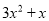 C.
C. 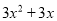 D.
D. 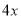
 C
【解析】利用因式分解是整式乘法的逆运算,可知=3x2+3x.
故选:C.
C
【解析】利用因式分解是整式乘法的逆运算,可知=3x2+3x.
故选:C.
练习册系列答案
相关题目
平移不改变图形的 ___________和 ___________
 形状 大小
【解析】试题解析:平移不改变图形的形状和大小.
故答案为:(1). 形状 (2). 大小.
形状 大小
【解析】试题解析:平移不改变图形的形状和大小.
故答案为:(1). 形状 (2). 大小. 如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
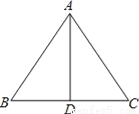
 ②③④
【解析】【解析】
应添加的条件是②③④;
证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高,则△ABD≌△ACD,∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF.
∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC,∴△AEF是等腰三角形,∴∠E=∠F.
∵AB=BE,∴∠A...
②③④
【解析】【解析】
应添加的条件是②③④;
证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高,则△ABD≌△ACD,∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF.
∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC,∴△AEF是等腰三角形,∴∠E=∠F.
∵AB=BE,∴∠A... 分解因式: 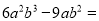 _______
_______
 【解析】根据提公因式法分解因式,可得=.
故答案为: .
【解析】根据提公因式法分解因式,可得=.
故答案为: . 用提公因式法分解因式: 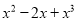 =__________
=__________
 【解析】根据提公因式法可以得到.
故答案为: .
【解析】根据提公因式法可以得到.
故答案为: . 多项式-6ab2+18a2b2-12a3b2c的公因式是( )
A.-6ab2c B.-ab2 C.-6ab2 D.-6a3b2c
 C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C.
C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C. 分解因式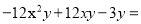 ___________
___________
 【解析】根据因式分解的方法,先提公因式-3y,再根据完全平方公式分解因式为: .
故答案为: .
【解析】根据因式分解的方法,先提公因式-3y,再根据完全平方公式分解因式为: .
故答案为: . 下列多项式,能用公式法分解因式的有( )
①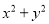 ②
②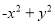 ③
③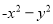 ④
④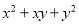
⑤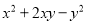 ⑥
⑥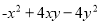
A. 2个 B. 3个 C. 4个 D. 5个
 A
【解析】根据完全平方公式,平方差公式,
的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A.
A
【解析】根据完全平方公式,平方差公式,
的特征可判定②可以利用平方差公式进行因式分解,⑥可以利用完全平方公式进行因式分解,因此本题正确选项是A. 已知有理式: 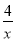 、
、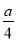 、
、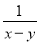 、
、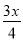 、
、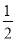 x2、
x2、 +4,其中分式有 ( )
+4,其中分式有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】、、、x2的分母中均不含有字母,因此它们是整式,而不是分式.
、、、+4的分母中含有字母,因此是分式.
所以B选项是正确的.
B
【解析】、、、x2的分母中均不含有字母,因此它们是整式,而不是分式.
、、、+4的分母中含有字母,因此是分式.
所以B选项是正确的.