题目内容
如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F的度数是（ ）
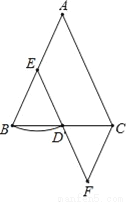
A. 40 B. 70 C. 50 D. 45
A
【解析】【解析】
∵以点E为圆心，EB为半径画弧，交BC于点D，∴EB=ED，∴∠EDB=∠B=70°，∴∠BED=180°﹣∠B=∠BDE=40°．
∵AB=AC，∴∠ACB=∠B，∴∠EDB=∠ACB，∴EF∥AC．
∵E是AB的中点，即BE=AE，∴BD=CD．
在△EBD和△FCD中，∵DE=DF，∠EDB=∠CDF，BD=CD，∴△EBD≌△FCD（SAS）...
练习册系列答案
相关题目
将一副直角三角尺如图放置，若∠AOD=20°， 则∠BOC的大小为（ ）
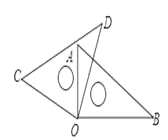
A. 140° B. 160° C. 170° D. 150°
B
【解析】试题分析：根据∠AOD=20°可得：∠AOC=70°，根据题意可得：∠BOC=∠AOB+∠AOC=90°+70°=160°. 若不等式ax-2＞0的解集为x＜-2，求关于y的方程ay+2=0的解
2
【解析】试题分析：根据不等式ax-2＞0的解集为x＜-2即可确定a的值，然后代入方程，解方程求得．
试题解析：∵不等式ax-2＞0，即ax＞2的解集为x＜-2，
∴a=-1，
代入方程得：-y+2=0，
解得：y=2． 如果（m+3）x＞2m+6的解集为x＜2，则m的取值范围是（ ）
A. m＜0 B. m＜-3 C. m＞-3 D. m是任意实数
B
【解析】由含有m的不等式（m+3）x＞2m+6的解集为：x＜2，根据不等式的基本性质3，可知m+3＜0，解得m＜-3.
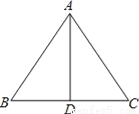
故选：B. 如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC是等腰三角形的是__．
①∠BAD=∠ACD；②∠BAD=∠CAD；③AB+BD=AC+CD；④AB﹣BD=AC﹣CD．
②③④
【解析】【解析】
应添加的条件是②③④；
证明：②当∠BAD=∠CAD时，∵AD是∠BAC的平分线，且AD是BC边上的高，则△ABD≌△ACD，∴△BAC是等腰三角形；
③延长DB至E，使BE=AB；延长DC至F，使CF=AC；连接AE、AF．
∵AB+BD=CD+AC，∴DE=DF，又AD⊥BC，∴△AEF是等腰三角形，∴∠E=∠F．
∵AB=BE，∴∠A... 分解因式：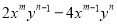 
（m,n均为大于1的整数）
【解析】试题分析：根据m,n均为大于1的整数，确定出指数最小的是哪一项，然后确定公因式再提取公因式即可.
试题解析： 分解因式：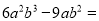 
_______
【解析】根据提公因式法分解因式，可得=.
故答案为： . 多项式-6ab2+18a2b2-12a3b2c的公因式是（ ）
A．-6ab2c B．-ab2 C．-6ab2 D．-6a3b2c
C
【解析】
试题分析：根据公因式的定义，先找出系数的最大公约数，相同字母的最低指数次幂，然后即可确定公因式．
多项式-6ab2+18a2b2-12a3b2c中，
系数的最大公约数是-6，
相同字母的最低指数次幂是ab2，
因此公因式是-6ab2，
故选C. 使两个直角三角形全等的条件是（ ）
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
D
【解析】试题分析：利用全等三角形的判定来确定．做题时，要结合已知条件与三角形全等的判定方法逐个验证．
【解析】
A、一个锐角对应相等，利用已知的直角相等，可得出另一组锐角相等，但不能证明两三角形全等，故A选项错误；
B、两个锐角相等，那么也就是三个对应角相等，但不能证明两三角形全等，故B选项错误；
C、一条边对应相等，再加一组直角相等，不能得出两三角形全等，故C选项错...