题目内容
如果x2+2(m-3)x+25能用公式法分解因式,那么m的值是多少?
 m=8或-2.
【解析】试题分析:利用完全平方公式的结构特征判断即可确定出m的值,注意包括两种情况.
试题解析:∵x2+2(m-3)x+25能用公式法分解因式,
∴2(m-3)=±10,
解得:m=8或-2.
m=8或-2.
【解析】试题分析:利用完全平方公式的结构特征判断即可确定出m的值,注意包括两种情况.
试题解析:∵x2+2(m-3)x+25能用公式法分解因式,
∴2(m-3)=±10,
解得:m=8或-2.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在下列实例中,不属于平移过程的有( )
①时针运行的过程;②火箭升空的过程;③地球自转的过程;④飞机从起跑到离开地面的过程
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】试题解析:①和③不属于平移,属于旋转.
故选B.
B
【解析】试题解析:①和③不属于平移,属于旋转.
故选B. 分解因式: 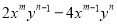 (m,n均为大于1的整数)
(m,n均为大于1的整数)
 【解析】试题分析:根据m,n均为大于1的整数,确定出指数最小的是哪一项,然后确定公因式再提取公因式即可.
试题解析:
【解析】试题分析:根据m,n均为大于1的整数,确定出指数最小的是哪一项,然后确定公因式再提取公因式即可.
试题解析: 把多项式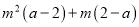 分解因式正确的是 ( )
分解因式正确的是 ( )
A.  B.
B. 
C.  D.
D. 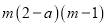
 B
【解析】根据因式分解法—提公因式,可由a-2与2-a互为相反数,先变形,再提公因式a-2可得: = = .
故选:B.
B
【解析】根据因式分解法—提公因式,可由a-2与2-a互为相反数,先变形,再提公因式a-2可得: = = .
故选:B. 多项式-6ab2+18a2b2-12a3b2c的公因式是( )
A.-6ab2c B.-ab2 C.-6ab2 D.-6a3b2c
 C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C.
C
【解析】
试题分析:根据公因式的定义,先找出系数的最大公约数,相同字母的最低指数次幂,然后即可确定公因式.
多项式-6ab2+18a2b2-12a3b2c中,
系数的最大公约数是-6,
相同字母的最低指数次幂是ab2,
因此公因式是-6ab2,
故选C. 因式分解: 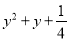 =______
=______
 【解析】根据完全平方公式进行因式分解为: .
故答案为:
.
【解析】根据完全平方公式进行因式分解为: .
故答案为:
. 下列式子分解因式能用公式法分解因式的是 ( ).
A. 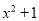 B.
B. 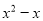 C.
C. 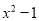 D.
D. 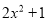
 C
【解析】根据平方差公式: ,可知因式分解为: .
故选:C.
C
【解析】根据平方差公式: ,可知因式分解为: .
故选:C. 如图,MN与PQ相交于点O,MO=OP,QO=ON,∠M=65°,∠Q=30°,则∠P=____,∠N=___.
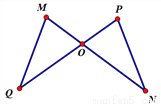
 65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30°
65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30° 根据不等式的基本性质,可将“mx<2”化为“x>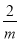 ”,则m的取值范围是_____.
”,则m的取值范围是_____.
 m<0
【解析】因为mx<2化为x>,
根据不等式的基本性质3得:m<0,
故答案为:m<0.
m<0
【解析】因为mx<2化为x>,
根据不等式的基本性质3得:m<0,
故答案为:m<0. 
