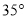题目内容
甲、乙两名学生练习计算机打字,甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同.已知甲每分钟比乙每分钟多打5个字,则乙每分钟打______个字.
 45
【解析】设乙每分钟打字x个,甲每分钟打个,根据题意可得: ,去分母可得:
,解得,经检验可得: ,故答案为:45.
45
【解析】设乙每分钟打字x个,甲每分钟打个,根据题意可得: ,去分母可得:
,解得,经检验可得: ,故答案为:45.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
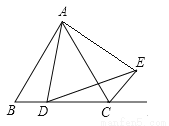
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图一,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上,
①求证:∠BCE+∠BAC=180°;
②当四边形ADCE的周长取最小值时,求BD的长.
(2)若∠BAC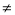 60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
 (1)①证明见解析;②BD=2;(2),理由见解析.
【解析】试题分析:
(1)∵
∴
又∵AB=AC,AD=AE
∴△ABD ≌ △ACE
∴
∴
(2)∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
(3)∴
理由如下:
∴ 又∵...
(1)①证明见解析;②BD=2;(2),理由见解析.
【解析】试题分析:
(1)∵
∴
又∵AB=AC,AD=AE
∴△ABD ≌ △ACE
∴
∴
(2)∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
(3)∴
理由如下:
∴ 又∵... 下列式子中,不是分式的是( )
A. 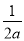 B.
B. 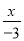 C.
C. 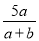 D.
D. 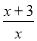
 B
【解析】根据分母中含有字母的式子是分式,即可进行判断.
【解析】
A. 分母中含有字母,是分式;
B. 分母中不含有字母,是整式;
C. 分母中含有字母,是分式;
D. . 分母中含有字母,是分式.
故选:B.
B
【解析】根据分母中含有字母的式子是分式,即可进行判断.
【解析】
A. 分母中含有字母,是分式;
B. 分母中不含有字母,是整式;
C. 分母中含有字母,是分式;
D. . 分母中含有字母,是分式.
故选:B. 无论a取何值时,下列分式一定有意义的是
A. 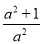 B.
B. 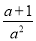 C.
C. 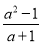 D.
D. 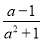
 D
【解析】试题解析:当a=0时,a2=0,故A、B中分式无意义;
当a=-1时,a+1=0,故C中分式无意义;
无论a取何值时,a2+1≠0,
故选D.
D
【解析】试题解析:当a=0时,a2=0,故A、B中分式无意义;
当a=-1时,a+1=0,故C中分式无意义;
无论a取何值时,a2+1≠0,
故选D. 为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
 甲:40,乙:60
【解析】试题分析:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品.根据题目中的等量关系“甲工厂单独加工完成这批产品的天数﹣乙工厂单独加工完成这批产品的天数=10”,列出方程解方程即可.
试题解析:【解析】
设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,
依题意得,
解得:x=40.
经检验:x=40是原方程的根,且符合题意....
甲:40,乙:60
【解析】试题分析:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品.根据题目中的等量关系“甲工厂单独加工完成这批产品的天数﹣乙工厂单独加工完成这批产品的天数=10”,列出方程解方程即可.
试题解析:【解析】
设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,
依题意得,
解得:x=40.
经检验:x=40是原方程的根,且符合题意.... 若分式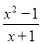 有意义,则x的取值范围为_________.
有意义,则x的取值范围为_________.
 x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1.
x≠-1
【解析】由题意得
x+1≠0,
∴x≠-1. 分式方程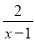 -
-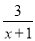 =0的解为( )
=0的解为( )
A. x=3 B. x=-5 C. x=5 D. 无解
 C
【解析】解方程-=0,方程两边同时乘以可得: ,去括号可得: ,移项合并同类项可得: 解得,经检验可得是原分式方程的根,故选C.
C
【解析】解方程-=0,方程两边同时乘以可得: ,去括号可得: ,移项合并同类项可得: 解得,经检验可得是原分式方程的根,故选C. 如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
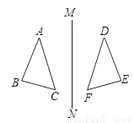
A. AB∥DF B. ∠B=∠E C. AB=DE D. AD的连线被MN垂直平分
 A
【解析】A选项无法判断;B. ∠B=∠E 、C. AB=DE 、 D. AD的连线被MN垂直平分均可以由成轴对称的两个图形的性质得到.
A
【解析】A选项无法判断;B. ∠B=∠E 、C. AB=DE 、 D. AD的连线被MN垂直平分均可以由成轴对称的两个图形的性质得到. 

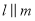 ,将含有
,将含有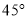 角的三角板
角的三角板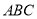 的直角顶点
的直角顶点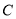 放在直线
放在直线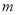 上,若
上,若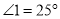 ,则
,则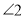 的度数为( )
的度数为( )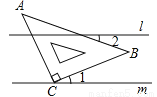
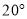 B.
B. 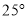 C.
C. 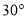 D.
D.