题目内容
用不等式表示“比x的5倍大1的数不小于x的一半”________.
 【解析】根据题意可得不等式.
【解析】根据题意可得不等式.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用为1000元/m2.设矩形的一边长为xm,面积为ym2.
(1)求出y与x之间的函数关系式,说明y是不是x的二次函数,并确定x的取值范围;
(2)若x=3时,广告牌的面积最大,求此时的广告费应为多少?
 (1)y=-x2+6x,是,0<x<6 ;(2)9000元
【解析】试题分析:
(1)矩形的一边长为xm,根据矩形的周长是12m,可得矩形的另一边长为(6-x)m,根据矩形的面积公式即可得出y与x之间的函数表达式;
(2)把x=3代入函数的解析式得出y的值即为广告牌的最大面积,再乘以1000即为此时的广告费.
试题解析:
【解析】
(1)由题意得出:y =x(6-x...
(1)y=-x2+6x,是,0<x<6 ;(2)9000元
【解析】试题分析:
(1)矩形的一边长为xm,根据矩形的周长是12m,可得矩形的另一边长为(6-x)m,根据矩形的面积公式即可得出y与x之间的函数表达式;
(2)把x=3代入函数的解析式得出y的值即为广告牌的最大面积,再乘以1000即为此时的广告费.
试题解析:
【解析】
(1)由题意得出:y =x(6-x... (5+x2)(5-x2)等于_______;
 25-x4
【解析】根据平方差公式可得:(5-x2)(5-x2)=25-x4.
25-x4
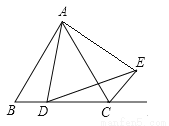
【解析】根据平方差公式可得:(5-x2)(5-x2)=25-x4. 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图一,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上,
①求证:∠BCE+∠BAC=180°;
②当四边形ADCE的周长取最小值时,求BD的长.
(2)若∠BAC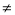 60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
 (1)①证明见解析;②BD=2;(2),理由见解析.
【解析】试题分析:
(1)∵
∴
又∵AB=AC,AD=AE
∴△ABD ≌ △ACE
∴
∴
(2)∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
(3)∴
理由如下:
∴ 又∵...
(1)①证明见解析;②BD=2;(2),理由见解析.
【解析】试题分析:
(1)∵
∴
又∵AB=AC,AD=AE
∴△ABD ≌ △ACE
∴
∴
(2)∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
(3)∴
理由如下:
∴ 又∵... 如图,点A2,A4…分别是x轴上的点,点A1,A3,A5,…分别是射线OA2n-1上的点,△OA1A2,△OA2A3,△OA3A4,…分别是以OA2,OA3,OA4 ,OA5…为底边的等腰三角形,若OA2n-1与x轴正半轴的夹角为30°,OA1=1,则可求得点A2的坐标是________;A2n-1的坐标_______.
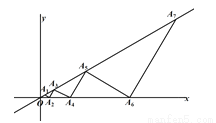
 【解析】根据等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,再由等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,由此可得A2n-1的坐标.
【解析】根据等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,再由等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,由此可得A2n-1的坐标. 已知图两个中三角形全等,则图2中的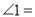 ( )
( )
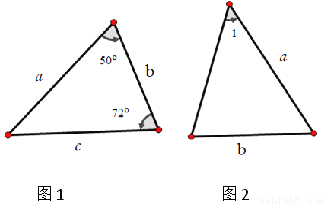
A. 50° B. 58° C. 60° D. 72°
 B
【解析】根据三角形的内角和定理求得∠2=180°-50°-72°=58°,根据全等三角形的对应角相等可得∠1=∠2=58°,故选B.
B
【解析】根据三角形的内角和定理求得∠2=180°-50°-72°=58°,根据全等三角形的对应角相等可得∠1=∠2=58°,故选B. 在代数式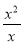 、
、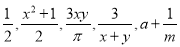 中,分式的个数有( )
中,分式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
 B
【解析】根据分式的定义,可以判断出题中六个代数式只有3个为分式,由此得出结论.
【解析】
在代数式、中,分式的有、,共3个.
故选B.
B
【解析】根据分式的定义,可以判断出题中六个代数式只有3个为分式,由此得出结论.
【解析】
在代数式、中,分式的有、,共3个.
故选B. 下列式子中,不是分式的是( )
A. 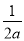 B.
B. 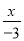 C.
C. 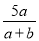 D.
D. 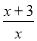
 B
【解析】根据分母中含有字母的式子是分式,即可进行判断.
【解析】
A. 分母中含有字母,是分式;
B. 分母中不含有字母,是整式;
C. 分母中含有字母,是分式;
D. . 分母中含有字母,是分式.
故选:B.
B
【解析】根据分母中含有字母的式子是分式,即可进行判断.
【解析】
A. 分母中含有字母,是分式;
B. 分母中不含有字母,是整式;
C. 分母中含有字母,是分式;
D. . 分母中含有字母,是分式.
故选:B. 分式方程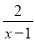 -
-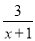 =0的解为( )
=0的解为( )
A. x=3 B. x=-5 C. x=5 D. 无解
 C
【解析】解方程-=0,方程两边同时乘以可得: ,去括号可得: ,移项合并同类项可得: 解得,经检验可得是原分式方程的根,故选C.
C
【解析】解方程-=0,方程两边同时乘以可得: ,去括号可得: ,移项合并同类项可得: 解得,经检验可得是原分式方程的根,故选C. 
