题目内容
 已知:如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
已知:如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.(1)求证:DF=CE;
(2)若DB⊥BE,垂足为B,BD=6,BE=8,求四边形AFBE的面积.
考点:全等三角形的判定与性质,三角形的面积
专题:几何综合题
分析:(1)先根据“AAS”证明△AOC≌△BOD,得到OC=OD,再根据线段中点即可证明DF=CE;
(2)由DB⊥BE,可得△DBE为直角三角形,再由BD=6,BE=8,求出△DBE的面积,再根据点E、F分别是OC、OD的中点,可得FD=OF=OE=CE,然后根据等底等高的三角形的面积相等可以得出S△DBF=S△FBO=S△OBE,进而求出△FOB或△OBE的面积,再证明四边形AEBF是平行四边形,即可确定其面积.
(2)由DB⊥BE,可得△DBE为直角三角形,再由BD=6,BE=8,求出△DBE的面积,再根据点E、F分别是OC、OD的中点,可得FD=OF=OE=CE,然后根据等底等高的三角形的面积相等可以得出S△DBF=S△FBO=S△OBE,进而求出△FOB或△OBE的面积,再证明四边形AEBF是平行四边形,即可确定其面积.
解答:(1)证明:∵AC∥BD,
∴∠C=∠D,∠CAO=∠DBO,AO=BO.
∴△AOC≌△BOD.
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴DF=
OD,CE=
OC.
∴DF=CE;
(2)解:∵∠DBE=90°,BD=6,BE=8,
∴S△BDE=
BD•BE=
×6×8=24,
∵E、F分别是OC、OD中点,
∴FD=OF=OE=CE,
∴S△BOF=
S△BDE=
×24=8,
∵AO=BO,OF=OE,
∴四边形AFBE是平行四边形,
∴四边形AFBE的面积=8×4=32.
∴∠C=∠D,∠CAO=∠DBO,AO=BO.
∴△AOC≌△BOD.
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=CE;
(2)解:∵∠DBE=90°,BD=6,BE=8,
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
∵E、F分别是OC、OD中点,
∴FD=OF=OE=CE,
∴S△BOF=
| 1 |
| 3 |
| 1 |
| 3 |
∵AO=BO,OF=OE,
∴四边形AFBE是平行四边形,
∴四边形AFBE的面积=8×4=32.
点评:本题主要考查了全等三角形、平行四边形的性质与判定,有一定的综合综合性,解决的关键是结合图形,认真分析,选择适当的方法判定三角形全等和平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若二次根式
在实数范围内有意义,则x的取值范围为( )
| 2x-4 |
| A、x≥2 | B、x≤3 |
| C、x≥-3 | D、x≤-3 |
如果点G是△ABC的重心,联结AG并延长,交对边BC于点D,那么AG:AD是( )
| A、2:3 | B、1:2 |
| C、1:3 | D、3:4 |
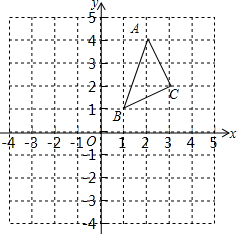 △ABC在平面直角坐标系中的位置如图所示(A、B、C三点在格点上),把△ABC绕原点O顺时针旋转90°,A、B、C旋转后的对应点分别是A1、B1、C1
△ABC在平面直角坐标系中的位置如图所示(A、B、C三点在格点上),把△ABC绕原点O顺时针旋转90°,A、B、C旋转后的对应点分别是A1、B1、C1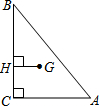 如图,已知在△ABC中,∠ACB=90°,AC=6,点G为重心,GH⊥BC,垂足为点H,那么GH=
如图,已知在△ABC中,∠ACB=90°,AC=6,点G为重心,GH⊥BC,垂足为点H,那么GH=