题目内容
如果点G是△ABC的重心，联结AG并延长，交对边BC于点D，那么AG：AD是（ ）
| A、2：3 | B、1：2 |
| C、1：3 | D、3：4 |
考点：三角形的重心
专题：
分析：根据三角形的重心到顶点的距离等于到对边中点的距离的2倍可得AG=2DG，那么AD=AG+DG=3DG，代入即可求得AG：AD的值．
解答：
解：如图，
∵点G是△ABC的重心，
∴AG=2DG，
∴AD=AG+DG=3DG，
∴
=
=
．
故选A．
解：如图，∵点G是△ABC的重心，
∴AG=2DG，
∴AD=AG+DG=3DG，
∴
| AG |
| AD |
| 2DG |
| 3DG |
| 2 |
| 3 |
故选A．
点评：本题考查了三角形的重心，熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
已知：如图，AB、CD相交于点O，AC∥DB，AO=BO，E、F分别是OC、OD中点．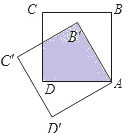
如图，正方形ABCD绕点A逆时针旋转，得到正方形AB′C′D′，当两正方形重叠部分的面积是原正方形面积的
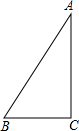如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕着点C旋转90°，点A、B的对应点分别是D、E，那么tan∠ADE的值
如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、D、F和点B、C、E，如果AD=6，DF=3，BC=5，那么BE=在Rt△ABC中，已知∠C=90°，AC=3，BC=4，那么∠A的余弦值等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线y=ax2+bx+c（a≠0）向右平移2个单位得到抛物线y=a（x-3）2-1，且平移后的抛物线经过点A（2，1）．