题目内容
将△ABC绕点A顺时针旋转50°,得到△ADE,直线BC与直线DE交于点F,则∠CFD等于 度.
考点:旋转的性质
专题:计算题
分析:分类讨论:当点F在BC边上,如图1,根据旋转的性质得∠DAC=50°,∠C=∠D,利用对顶角相等得∠CAG=∠FGD,然后根据三角形内角和定理即可得到∠GFD=∠GAC=50°,即∠CFD=50°;当点F在BC边的延长线上,如图2,根据旋转的性质得∠DAC=50°,∠C=∠ADE,利用邻补角得到∠ADE+∠ADF=180°,则∠C+∠ADF=180°,然后根据四边形内角和可计算出∠CFD=130°,综上所述,∠CFD等于50度或130度.
解答:解:当点F在BC边上,如图1,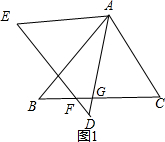
∵将△ABC绕点A顺时针旋转50°,得到△ADE,
∴∠DAC=50°,∠C=∠D,
∵∠CAG=∠FGD,
∴∠GFD=∠GAC=50°,即∠CFD=50°;
当点F在BC边的延长线上,如图2,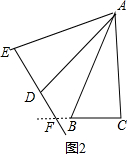
∵将△ABC绕点A顺时针旋转50°,得到△ADE,
∴∠DAC=50°,∠C=∠ADE,
∵∠ADE+∠ADF=180°,
∴∠C+∠ADF=180°,
∴∠CFD+∠DAC=180°,
∴∠CFD=180°-50°=130°,
综上所述,∠CFD等于50度或130度.
故答案为50度或130.

∵将△ABC绕点A顺时针旋转50°,得到△ADE,
∴∠DAC=50°,∠C=∠D,
∵∠CAG=∠FGD,
∴∠GFD=∠GAC=50°,即∠CFD=50°;
当点F在BC边的延长线上,如图2,

∵将△ABC绕点A顺时针旋转50°,得到△ADE,
∴∠DAC=50°,∠C=∠ADE,
∵∠ADE+∠ADF=180°,
∴∠C+∠ADF=180°,
∴∠CFD+∠DAC=180°,
∴∠CFD=180°-50°=130°,
综上所述,∠CFD等于50度或130度.
故答案为50度或130.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
下列代数式中,互为同类项的是( )
| A、-2a2b与3ab2 |
| B、18x2y2与9x2+2y2 |
| C、a+b与a-b |
| D、-xy2与y2x |
西安世界园艺博览会园区占地面积约为418公顷(1公顷=104平方米),它的百分之一相当于( )的面积.
| A、我们的教室 |
| B、我们的黑板 |
| C、我们的课桌 |
| D、我们的数学课本 |
 在平面直角坐标系中,已知点A(-4,2),B(-4,0),C(-1,1),请在图上画出△ABC,并画出与△ABC关于原点O对称的图形.
在平面直角坐标系中,已知点A(-4,2),B(-4,0),C(-1,1),请在图上画出△ABC,并画出与△ABC关于原点O对称的图形. 如图,△ABC是直角三角形,∠C=90°,将△ABC绕点C顺时针旋转90°.
如图,△ABC是直角三角形,∠C=90°,将△ABC绕点C顺时针旋转90°. 已知:如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
已知:如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.