题目内容
17. 某电信公司为顾客提供了A,B两种手机上网方式,一个月的手机上网费用y(元)与上网时间x(分钟)之间的关系如图,如果一个月上网300分钟,那么方式B产生的费用比方式A高8元.
某电信公司为顾客提供了A,B两种手机上网方式,一个月的手机上网费用y(元)与上网时间x(分钟)之间的关系如图,如果一个月上网300分钟,那么方式B产生的费用比方式A高8元.
分析 设yA=kAx,yB=kBx+20,求得x=500时,kB-kA=-$\frac{1}{25}$,然后x=300求得结果.
解答 解:设yA=kAx,yB=kBx+20,
当x=500时,yA=yB,即500kA=500kB+20,
∴kB-kA=-$\frac{1}{25}$,
当x=300时,yB-yA=300kB+20-300kA=300(kB-kA)+20=8,
∴如果一个月上网300分钟,那么方式B产生的费用比方式A高8元,
故答案为:8.
点评 本题考查了一次函数的应用,正确的识别图象是解题的关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.在${({-\sqrt{2}})^0}$,0,$\sqrt{9}$,$-\frac{π}{3}$,-0.333…,$\sqrt{5}$,3.1415926,0.010010001…(相邻两个1之间依次多1个0)中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
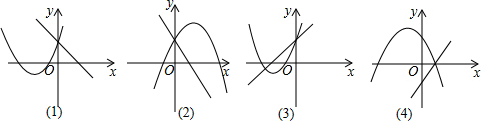

| A. | (4) | B. | (1),(4) | C. | (2),(3) | D. | (3),(4) |
 (1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC
(1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC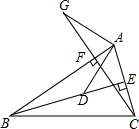 如图,已知在△ABC中,BE、CF分别是AC、AB边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG,则AG与AD有何关系?试证明你的结论.
如图,已知在△ABC中,BE、CF分别是AC、AB边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG,则AG与AD有何关系?试证明你的结论. 如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.
如图,AC、BC分别平分∠MAB和∠ABN,∠ACB=90°.