题目内容
8. (1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC
(1)在等腰梯形ABCD中,若AD∥BC,PA=PD.求证:PB=PC(2)在上面的题目中的“等腰梯形ABCD”设为另一个四边形,其余条件不变,使PB=PC仍然成立.应改成一个什么样的四边形,请画出图形.并写出已知、求证.
分析 (1)根据等腰梯形的性质得到AB、CD相等,∠BAD=∠CDA,根据全等三角形的性质即可得到结论;
(2)根据题意写出命题即可.
解答 证明:∵ABCD是等腰梯形,
∴AB=DC,∠BAD=∠CDA,
又∵PA=PD,
∴∠PAD=∠PDA,
∵∠PAB=∠BAD-∠PAD,∠PDC=∠CDA-∠PDA,
∴∠PAB=∠PDC,
在△PAB和△PDC中$\left\{\begin{array}{l}{AB=DC}\\{∠PAB=∠PDC}\\{PA=PD}\end{array}\right.$,
∴△PAB≌△PDC(SAS),
∴PB=PC;
(2)已知:如图所示,在矩形ABCD所在平面有一点P,且PA=PD,求证:PB=PC.
点评 此题考查了等腰梯形的性质、全等三角形的判定与性质,关键在于用好等腰梯形的性质,得出三角形全等的条件,从而得出全等三角形的对应边相等.

练习册系列答案
相关题目
18.已知∠ABC=45°,D为BC上一点,请在AB上找一点E,连接DE,使得∠BDE=45°.图1,2分别是甲、乙两名同学的作法,则下列说法正确的是( )
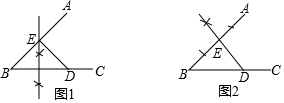
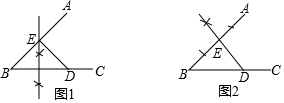
| A. | 甲、乙两名同学的作法均正确 | |
| B. | 甲、乙两名同学的作法均不正确 | |
| C. | 甲同学的作法正确,乙同学的作法不正确 | |
| D. | 甲同学的作法不正确,乙同学的作法正确 |
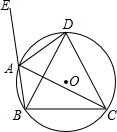 如图,AD是圆内接△ABC的∠BAC的外角平分线,交圆于点D.求证:△BDC是等腰三角形.
如图,AD是圆内接△ABC的∠BAC的外角平分线,交圆于点D.求证:△BDC是等腰三角形. 如图,点A、C为反比例函数y=$\frac{k}{x}$(x<0)图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为$\frac{3}{2}$时,求k的值.
如图,点A、C为反比例函数y=$\frac{k}{x}$(x<0)图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为$\frac{3}{2}$时,求k的值. 如图,PA,PB分别与⊙O相切于点A,B,AC是⊙O的直径,若tan∠ACB=$\sqrt{5}$,求tan∠PCB的值.
如图,PA,PB分别与⊙O相切于点A,B,AC是⊙O的直径,若tan∠ACB=$\sqrt{5}$,求tan∠PCB的值.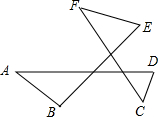 如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.
如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.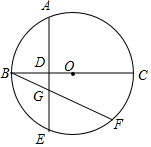 如图,BC是⊙O的直径,弦AE⊥BC,垂足为D点,$\widehat{AB}$=$\frac{1}{2}$$\widehat{BF}$,AE与BF相交于G点.
如图,BC是⊙O的直径,弦AE⊥BC,垂足为D点,$\widehat{AB}$=$\frac{1}{2}$$\widehat{BF}$,AE与BF相交于G点. 如图,△ABC中,∠BAC=90°,D在BC上,DE⊥AB于E,DF⊥AC于F,DE=DF.
如图,△ABC中,∠BAC=90°,D在BC上,DE⊥AB于E,DF⊥AC于F,DE=DF. 某电信公司为顾客提供了A,B两种手机上网方式,一个月的手机上网费用y(元)与上网时间x(分钟)之间的关系如图,如果一个月上网300分钟,那么方式B产生的费用比方式A高8元.
某电信公司为顾客提供了A,B两种手机上网方式,一个月的手机上网费用y(元)与上网时间x(分钟)之间的关系如图,如果一个月上网300分钟,那么方式B产生的费用比方式A高8元.