题目内容
13.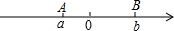 数学实验室:
数学实验室:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
利用数形结合思想回答下列问题:
①数轴上表示2和5两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4.
②数轴上表示x和-2的两点之间的距离表示为|x+2|.数轴上表示x和5的两点之间的距离表示为|5-x|.
③若x表示一个有理数,则|x-1|+|x+3|的最小值=4.
④若x表示一个有理数,且|x+3|+|x-2|=5,则满足条件的所有整数x的是-3或2或-1或0或1或2.
⑤若x表示一个有理数,当x为3,式子|x+2|+|x-3|+|x-5|有最小值为7.
分析 ①②在数轴上A、B两点之间的距离AB=|a-b|,依此即可求解;
④根据绝对值的性质去掉绝对值号,然后计算即可得解;
③首先将原式变形为y=|x-1|+|x+3|,然后分别从当x≥1时,当-3≤x<1时,当x<-3时去分析,根据一次函数的增减性,即可求得y的最小值;
④当x<-3时,当-3≤x≤2时,当x>2时,当x=-1,当x=1,当x=0去分析,根据一次函数的增减性,即可求得答案;
⑤当x≥5时,当3≤x<5时,当-2≤x<3时,当x<-2时去分析,根据一次函数的增减性,即可求得y的最小值.
解答 解:①数轴上表示2和5两点之间的距离是5-2=3,数轴上表示1和-3的两点之间的距离是1-(-3)=4,
故答案为:3,4;
②数轴上表示x和-2的两点之间的距离表示为|x-(-2)|=|x+2|,数轴上表示x和5的两点之间的距离表示为|5-x|,
故答案为:|x+2|,|5-x|;
③当x<-3时,|x-1|+|x+3|=1-x-x-3=-2x-2,
当-3≤x≤1时,|x-1|+|x+3|=1-x+x+3=4,
当x>1时,|x-1|+|x+3|=x-1+x+3=2x+2,
在数轴上|x-1|+|x+3|的几何意义是:表示有理数x的点到-3及到1的距离之和,所以当-3≤x≤1时,它的最小值为4,
故答案为:4;
④当x<-3时,|x+3|+|x-2|=-x-3+2-x=-2x-1=5,
解得:x=-3,
此时不符合x<-3,舍去;
当-3≤x≤2时,|x+3|+|x-2|=x+3+2-x=5,
此时x=-3或x=2;
当x>2时,|x+3|+|x-2|=x+3+x-2=2x+1=5,
解得:x=2,
此时不符合x>2,舍去;
当x=0时,|x+3|+|x-2|=5;
当x=1时,|x+3|+|x-2|=5;
当x=-1时,|x+3|+|x-2|=5;
故答案为:-3或2或-1或0或1或2;
⑤∵设y=|x+2|+|x-3|+|x-5|,
i、当x≥5时,y=x+2+x-3+x-5=3x-6,
∴当x=5时,y最小为:3x-6=3×5-6=9;
ii、当3≤x<5时,y=x+2+x-3+5-x=x+4,
∴当x=3时,y最小为7;
iii、当-2≤x<3时,y=x+2+3-x+5-x=10-x,
∴此时y最小接近7;
iiii、当x<-2时,y=-x-2+3-x+5-x=6-x,
∴此时y最小接近8;
∴y的最小值为7.
故答案为:3,7.
点评 本题考查了数轴,绝对值的性质,读懂题目信息,理解数轴上两点间的距离的表示是解题的关键.注意分类思想的运用.

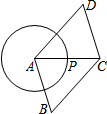 如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )
如图,点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=$\sqrt{3}$,则平行四边形ABCD面积的最大值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{3}$ |
| A. | 它的图象是一条直线 | B. | 它的图象经过原点 | ||
| C. | 它的图象在第一、三象限 | D. | 在每个象限内,y随x的增大而增大 |
| A. | y=(x-3)2-2 | B. | y=(x-1)2+4 | C. | y=(x-3)2+4 | D. | y=(x-2)2-2 |
| A. | x | B. | y | ||
| C. | 两个中的任何一个都一样 | D. | 无法确定 |