题目内容
18．将抛物线y=（x-2）2+1向右平移1个单位，再向上平移3个单位后所得抛物线的表达式为（ ）| A． | y=（x-3）2-2 | B． | y=（x-1）2+4 | C． | y=（x-3）2+4 | D． | y=（x-2）2-2 |
分析 根据“左加右减，上加下减”的规律即可求得．
解答 解：因为抛物线y=（x-2）2+1向右平移1个单位，得：y=（x-2-1）2+1，
再向上平移3个单位得：y=（x-2-1）2+1+3，即：y=（x-3）2+4．
故选C．
点评 此题考查函数图象平移与函数解析式的变化规律，要求能总结平移规律：“左加右减，上加下减”，并依据此规律求平移前后的函数解析式．
练习册系列答案
名校课堂系列答案
相关题目
9．
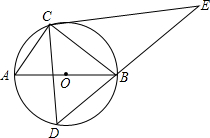如图，定点C、动点D在⊙O上，并且位于直径AB的两侧，AB=10，AC=6，过点C在作CE⊥CD交DB的延长线于点E，则线段CE长度的最大值为（ ）
如图，定点C、动点D在⊙O上，并且位于直径AB的两侧，AB=10，AC=6，过点C在作CE⊥CD交DB的延长线于点E，则线段CE长度的最大值为（ ）| A． | $\frac{20}{3}$ | B． | $\frac{40}{3}$ | C． | 16 | D． | $\frac{64}{5}$ |
数学实验室：