题目内容
15.甲、乙两车分别从相距360km的 A、B两地出发,甲车速度为70km/h,乙车速度为50km/h.(1)两车同时出发,相向而行,经过多长时间两车相遇?
(2)两车同时出发,同向而行(乙车在前甲车在后),经过多长时间两车相遇?
(3)两车同时出发,同向而行,多长时间后两车相距60km?
分析 (1)设两车同时出发,相向而行,经过x小时两车相遇,由题意得等量关系:甲乙两车的速度和×行驶时间=360km,根据等量关系列出方程,再解即可;
(2)设两车同时出发,同向而行(乙车在前甲车在后),经过y小时两车相遇,由题意得等量关系:甲乙两车的速度差×行驶时间=360km,根据等量关系列出方程,再解即可;
(3)设两车同时出发,同向而行,z小时后两车相距60km,此题要分两种情况:①相遇前,甲乙两车路程差=360-60,②相遇后甲乙两车路程差=360+60,根据等量关系列出方程,再解即可.
解答 解:(1)设两车同时出发,相向而行,经过x小时两车相遇,由题意得:
(70+50)x=360,
解得:x=3.
答:两车同时出发,相向而行,经过3小时两车相遇.
(2)设两车同时出发,同向而行(乙车在前甲车在后),经过y小时两车相遇,由题意得:
70y-50y=360,
解得:y=18.
答:经过18小时两车相遇;
(3)设两车同时出发,同向而行,z小时后两车相距60km,
①相遇前:70z-50z=360-60,
解得:z=15,
②相遇后:70z-50z=360+60,
解得:z=21.
答:两车同时出发,同向而行,15小时或21小时后两车相距60km.
点评 此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在直角坐标系中,已知A(1,1),在坐标轴上确定一点P,使得△AOP为等腰三角形,则符合条件的点P共有( )
| A. | 4个 | B. | 6个 | C. | 8个 | D. | 10个 |
4.若点(3,-4)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点中,在此函数图象上的是( )
| A. | (-3,4) | B. | (-2,-6) | C. | (-6,-2) | D. | (-3,-4) |
5.已知圆锥底面直径为80cm,母线长为90cm,则圆锥侧面积为( )
| A. | 3600. | B. | 3600π | C. | 1800π | D. | 3000π |
 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.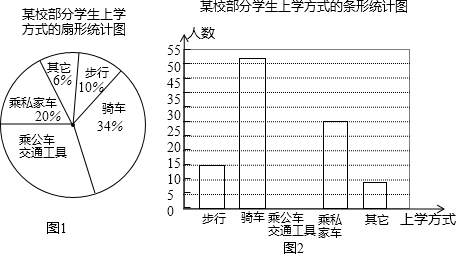
 如图所示,根据图中信息完成问题.
如图所示,根据图中信息完成问题.