题目内容
7.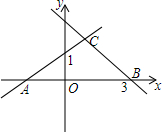 如图所示,根据图中信息完成问题.
如图所示,根据图中信息完成问题.(1)求出点C的坐标;
(2)当x为何值时,y1>y2?
分析 (1)根据题意,函数y1=x+n与y2=-x+m分别过点(0,1)和点(3,0),把其代入函数的解析式,可以写出m,n的值,从而求出两函数的解析式,联立方程可以求出两函数的交点;
(2)求出两函数的交点后,根据一次函数的性质,可以求出y1>y2时,x的范围;
解答 解:(1)∵函数y1=x+n过点(0,1)代入y1得:n=1,
∵函数y2=-x+m过点(3,0),代入y2得:-3+m=0,
∴m=3;
∴y1=x+1,y2=-x+3,
∴x+1=-x+3,
∴x=1,把x=1代入y1得,
y1=2,
∴两函数的交点为(1,2),
即P(1,2);
(2)由一次函数的图象知,当函数y1的图象在y2的上面时,有x>1,
∴当x>1时,y1>y2.
点评 此题考查了两条直线相交或平行问题,待定系数法求解析式以及一次函数的基本性质,根据待定系数法求得两直线的解析式是解题的关键.

练习册系列答案
相关题目
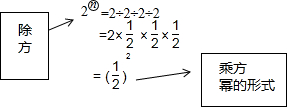 概念学习
概念学习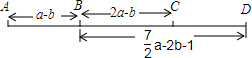
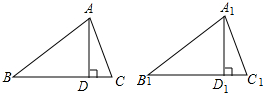 如图所示,AD、A1D1分别是锐角△ABC和△A1B1C1中边BC、B1C1的高,且AB=A1B1,AD=A1D1,若要使△ABC≌△A1B1C1,可补充的条件是∠C=∠C1(只需要填写一个你认为适当的条件即可)
如图所示,AD、A1D1分别是锐角△ABC和△A1B1C1中边BC、B1C1的高,且AB=A1B1,AD=A1D1,若要使△ABC≌△A1B1C1,可补充的条件是∠C=∠C1(只需要填写一个你认为适当的条件即可)