题目内容
5. 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.(1)当∠CAD=30°时,∠BAC=(60)°.
(2)当∠DAE=48°时,求∠CAD的度数.
理由如下:由∠BAD=90°与∠DAE=48°,可得∠BAE=(138)°
由射线AC平分∠BAE,可得∠CAE=∠BAC=(69)°
所以,∠CAD=(21)°.
分析 (1)直接利用∠BAD=90°,∠CAD=30°,求出答案即可;
(2)结合已知利用角平分线的性质得出答案.
解答 解:(1)∵∠BAD=90°,∠CAD=30°,
∴∠BAC=90°-30°=60°;
故答案为:60;
(2)由∠BAD=90°与∠DAE=48°,可得∠BAE=138°
由射线AC平分∠BAE,可得∠CAE=∠BAC=69°
所以,∠CAD=21°.
故答案为:138,69,21.
点评 此题主要考查了角平分线的定义以及互余两角的定义,正确应用角平分线的性质是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.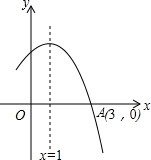 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③当x<1时,y随x的增大而增大;④方程ax2+bx+c=0的根为x1=-1,x2=3;⑤4a-2b+c>0其中正确结论是( )| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ③④⑤ |
14.数轴的三要素是( )
| A. | 原点、方向、单位长度 | B. | 直线、方向、单位长度 | ||
| C. | 直线、原点、方向 | D. | 直线、单位长度、原点 |
 如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.
如图所示,已知△ABC的周长是20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是30.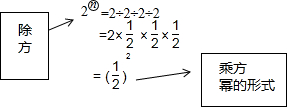 概念学习
概念学习