题目内容
12.(1)已知mn-n=15,m-mn=6,求:代数式m-n的值;(2)已知x2+2x-5=3,求:代数式2x2+4x+8的值;
(3)已知x2-x-1=0,求:代数式-x3+2x2+2015的值.
分析 (1)两式相加即可求得答案.
(2)先求出x2+2x的值,然后整体代入进行计算即可得解.
(3)由x2-x-1=0,得到x2=x+1,-x2+x=-1;将所给的代数式变形、化简、求值,即可解决问题.
解答 解:(1)∵mn-n=15,m-mn=6,
∴两式相加得到:m-n=21;
(2)∵x2+2x-5=3,
∴x2+2x=8,
∴2x2+4x+8=2(x2+2x)+8=24;
(3)∵x2-x-1=0,
∴x2=x+1,-x2+x=-1,
∴-x3+2x+2015
=-x(x+1)+2x+2015
=-x2-x+2x+2015
=-x2+x+2015
=2014.
点评 该题主要考查了因式分解在代数式的化简、求值等方面的应用问题;解题的关键是运用因式分解法,灵活将所给的条件、所要化简的代数式变形、化简、运算、求值.

练习册系列答案
相关题目
5.下列四条线段中,不能成比例的是( )
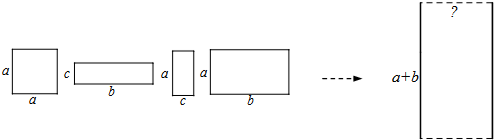
| A. | a=3,b=6,c=2,d=4 | B. | a=1,b=$\sqrt{2}$,c=2$\sqrt{2}$,d=4 | ||
| C. | a=4,b=5,c=8,d=10 | D. | a=2,b=3,c=4,d=5 |
1.某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入-维护费用)
(1)填表(不需化简)
| 入住的房间数量 | 房间价格 | 总维护费用 | |
| 提价前 | 60 | 200 | 60×20 |
| 提价后 | 60-$\frac{x}{10}$ | 200+x | (60-$\frac{x}{10}$)×20 |
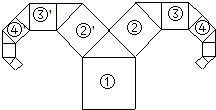 如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.
如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.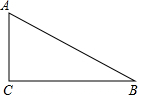 用直尺、圆规作图,不写作法,但要保留作图痕迹.
用直尺、圆规作图,不写作法,但要保留作图痕迹.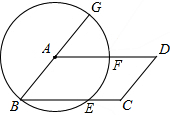 如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.
如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.