题目内容
2.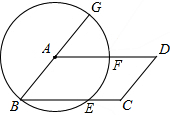 如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.
如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧$\widehat{EF}$和弧$\widehat{FG}$是否相等,并说明理由.
分析 要证明$\widehat{EF}$=$\widehat{FG}$,则要证明∠DAF=∠GAD,由AB=AF,得出∠ABF=∠AFB,平行四边形的性质得出,∠AFB=∠DAF,∠GAD=∠ABF,由圆心角、弧、弦的关系定理得出$\widehat{EF}$=$\widehat{FG}$.
解答  解:$\widehat{EF}$=$\widehat{FG}$,
解:$\widehat{EF}$=$\widehat{FG}$,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴$\widehat{EF}=\widehat{FG}$.
点评 本题考查了平行四边形性质,平行线性质,圆心角、弧、弦的关系定理等知识点的应用,关键是求出∠DAF=∠GAD,题目比较典型,难度不大.

练习册系列答案
相关题目
10.某汽车销售公司2013年盈利1500万元,2015年盈利2160万元,且从2013年到2015年,每年盈利的年增长率相同.设每年盈利的年增长率为x,根据题意,所列方程正确的是( )
| A. | 1500(1+x)+1500(1+x)2=2160 | B. | 1500x+1500x2=2160 | ||
| C. | 1500x2=2160 | D. | 1500(1+x)2=2160 |
14.下列说法正确的是( )
| A. | 1的立方根是±1 | B. | $\sqrt{16}$±4 | C. | $\sqrt{16}$=4 | D. | 0没有平方根 |
 如图,已知二次函数y=x2-4x-5与x轴交于A,B两点,则AB的长度为6.
如图,已知二次函数y=x2-4x-5与x轴交于A,B两点,则AB的长度为6. 有理数a、b在数轴上的对应点位置如图所示
有理数a、b在数轴上的对应点位置如图所示 如图,池塘边有一块长为20米,宽为12米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:
如图,池塘边有一块长为20米,宽为12米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示: