题目内容
13.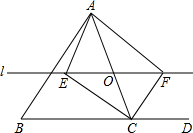 如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.
如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.(1)OE与OF相等吗?证明你的结论.
(2)试确定点O的位置,使四边形AECF是矩形,并加以证明.
分析 (1)根据平行线性质和角平分线定义推出∠OEC=∠OCE,∠OFC=∠OCF,根据等腰三角形的判定推出OE=OC,OF=OC即可;
(2)根据平行四边形的判定得出平行四边形AECF,根据对角线相等的平行四边形是矩形推出即可;
解答 (1)解:相等;理由是:∵直线l∥BC,
∴∠OEC=∠ECB,
∵CE平分∠ACB,
∴∠OCE=∠BCE,
∴∠OEC=∠OCE,
∴OE=OC,
同理OF=OC,
∴OE=OF.
(2)解:O在AC的中点上时,四边形AECF是矩形,
理由是:∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵OE=OF=OC=OA,
∴AC=EF,
∴平行四边形AECF是矩形.
点评 本题综合考查了平行四边形的性质和判定,矩形的判定,平行线的性质,角平分线定义等知识点的应用,题型较好,综合性比较强,难度也适中.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.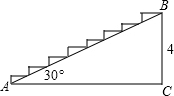 现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
 现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)| A. | 6.9m | B. | 4m | C. | 8m | D. | 10.9m |
2.下列事件是随机事件的是( )
| A. | 两个整数相加,和是整数 | B. | 两个整数相减,差是整数 | ||
| C. | 两个整数相乘,积是整数 | D. | 两个整数相除,商是整数 |
 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.