题目内容
3. 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.(1)求证:AE⊥DE;
(2)若tan∠CBA=2,AE=4,求AF的长.
分析 (1)首先连接OC,由OC=OA,$\widehat{BC}$=$\widehat{FC}$,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;
(2)首先证明ACE=∠ABC,由tan∠CBA=tan∠ACE=2=$\frac{AE}{EC}$,AE=4,推出EC=2,根据EC2=EF•EA,求出EF即可解决问题.
解答 (1)证明:连接OC,
∵OC=OA,
∴∠BAC=∠OCA,
∵$\widehat{BC}$=$\widehat{FC}$,
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵DE切⊙O于点C,
∴OC⊥DE.
∴AE⊥DE;
(2)解:连接CF.
∵$\widehat{BC}$=$\widehat{FC}$,
∴∠CAB=∠CAE,
∵∠CAB+∠ABC=90°,∠ACE+∠ACE=90°,
∴∠ACE=∠ABC,
∵tan∠CBA=tan∠ACE=2=$\frac{AE}{EC}$,
∵AE=4,
∴EC=2,
∵EC2=EF•EA,
∴22=EF•4,
∴EF=1,
∴AF=AE-EF=3.
点评 此题考查了切线的性质、直角三角形的性质、圆周角定理、切割线定理、锐角三角函数、平行线的性质等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
11.我国自主研发的“天宫二号”对接成功,标志着我国航天事业又上了一个新台阶,“天宫二号”火箭的飞行速度约为每秒8千米,也就是28800千米/时,“28800”用科学记数法表示为( )
| A. | 2.88×102 | B. | 28.8×103 | C. | 2.88×104 | D. | 0.288×105 |
12.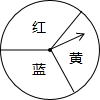 如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )
如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )
 如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )
如果身边没有质地均匀的硬币,下列方法可以模拟掷硬币实验的是( )| A. | 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面 | |
| B. | 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面 | |
| C. | 掷一枚质地均匀的骰子,奇数点朝上代表正面,偶数点朝上代表反面 | |
| D. | 转动如图所示的转盘,指针指向“红”代表正面,指针指向“蓝”代表反面 |
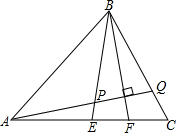 如图,△ABC中,BE为AC边的中线,BF平分∠EBC,AQ⊥BF交BE于P,交BC于Q,求$\frac{EP}{CQ}$.
如图,△ABC中,BE为AC边的中线,BF平分∠EBC,AQ⊥BF交BE于P,交BC于Q,求$\frac{EP}{CQ}$.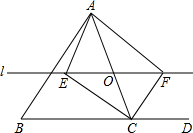 如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.
如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.