题目内容
5.一列式子按一定规律排列:-$\frac{a}{2}$,$\frac{a^3}{4}$,-$\frac{a^5}{6}$,$\frac{a^7}{8}$,…,则第5个式子是-$\frac{{a}^{9}}{10}$,则第n个式子是(-1)n$\frac{{a}^{2n-1}}{2n}$.分析 系数的规律是-$\frac{1}{2}$,$\frac{1}{4}$,-$\frac{1}{6}$,$\frac{1}{8}$…,指数的规律是1,3,5,7…,
解答 解:根据题意可知第n的式子为:(-1)n$\frac{{a}^{2n-1}}{2n}$
当n=5时,
该单项式为:-$\frac{{a}^{9}}{10}$
故答案为:$-\frac{a^9}{10}$,${(-1)^n}\frac{{{a^{2n-1}}}}{2n}$
点评 本题考查数字规律,解题的关键是根据题意找出单项式之间的规律,本题属于基础题型.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
10.全国“双创周”活动在深圳湾创业广场启幕,未来三年,国家将投入8500亿元用于大众创业万众创新,将8500亿元用科学记数法表示为( )
| A. | 8.5×103亿元 | B. | 0.85×104亿元 | C. | 8.5×104亿元 | D. | 85×102亿元 |
15.下列各图是立体图形的是( )
| A. |  | B. |  | C. |  | D. |  |
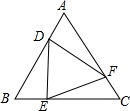 如图,等边△ABC中,点D,E,F分别同时从点A,B,C出发,以相同的速度在AB,BC,CA上运动,连结DE,EF,DF.
如图,等边△ABC中,点D,E,F分别同时从点A,B,C出发,以相同的速度在AB,BC,CA上运动,连结DE,EF,DF.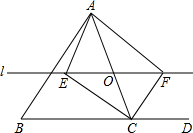 如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.
如图,在△ABC中,O是AC上的任意一点(不与点A、C重合),过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.