题目内容
13.若甲每小时走4千米,出发3小时后,乙开车要在20分钟内追上甲,问乙的车速至少是多少?(列不等式解答)分析 设乙的车速是x千米/小时,则依据“乙开车要在20分钟内追上甲”列出不等式.
解答 解:乙的车速是x千米/小时,
依题意得4×(3+$\frac{1}{3}$)≤$\frac{1}{3}$x,
解得 x≥40,
则x的最小值是40,即乙的车速至少是40千米/小时.
答:乙的车速至少是40千米/小时.
点评 本题考查了一元一次不等式的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的不等关系.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
| A. | 1 | B. | 1或$\frac{\sqrt{3}-1}{2}$ | C. | 1或$\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$ |
2.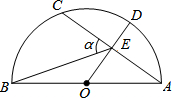 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )| A. | $\frac{3\sqrt{13}}{13}$ | B. | $\frac{2\sqrt{13}}{13}$ | C. | $\frac{\sqrt{13}}{13}$ | D. | $\frac{2}{3}$ |
3.某县为发展教育事业,加强了对教育经费的投入,2013年投入5000万元,预计2015年投入8000万元.设教育经费连续两年的年平均增长率为x,根据题意,下面所列方程正确的是( )
| A. | 5000(1+x)2=8000 | B. | 5000x2=8000 | ||
| C. | 5000(1+x%)2=8000 | D. | 5000(1+x)+5000(1+x)2=8000 |
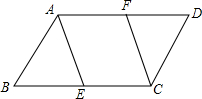 如图,在?ABCD中,点E、F分别是BC、AD的中点
如图,在?ABCD中,点E、F分别是BC、AD的中点