题目内容
11.若x2+4y2-6x+4y+10=0,则yx=-$\frac{1}{8}$.分析 先利用完全平方公式把x2+4y2-6x+4y+10=0,变为(x-3)2+4(y+$\frac{1}{2}$)2=0,利用非负数的性质得出x、y的数值,进一步代入求得答案即可.
解答 解:∵x2+4y2-6x+4y+10=0,
∴(x-3)2+4(y+$\frac{1}{2}$)2=0,
则x-3=0且y+$\frac{1}{2}$=0,
解得x=3,y=-$\frac{1}{2}$.
∴yx=(-$\frac{1}{2}$)3=-$\frac{1}{8}$.
故答案是:-$\frac{1}{8}$.
点评 本题考查了配方法的应用,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
1.一组数据包含2,4,x,4,4共5个数,它们的平均数是4,则这组数据的中位数和方差分别是( )
| A. | 2和1.6 | B. | 4和1.6 | C. | 4和8 | D. | 6和1.6 |
16.线段AB=3cm,BC=6cm,则A、C两点之间的距离是( )
| A. | 9cm | B. | 3cm | C. | 9cm或3cm | D. | 不能确定 |
3.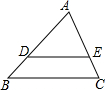 如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
 如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
20. 如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )
如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )
 如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )
如图线段AB,延长线段AB至C,使BC=3AB,取BC中点D,则( )| A. | AD=CD | B. | AD=BC | C. | DC=2AB | D. | AB:BD=2:3 |