题目内容
4. 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\frac{8}{3}$$\sqrt{10}$ |
分析 如图将△BCE绕点B逆时针旋转90°得到△BAM.BF与AD交于点G.首先证明GE=AG+CE,设AG=x,在Rt△DGE中,利用勾股定理求出x,再证明BG=FG,求出BG即可解决问题.
解答 解:如图将△BCE绕点B逆时针旋转90°得到△BAM.BF与AD交于点G.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=3,∠ABC=90°,
∵∠GBE=45°,
∴∠CBE+∠GBA=∠ABM+∠GBA=45°=∠GBM,
∵BG=BG,∠GBM=∠GBE,BE=BM,
∴△BGM≌△BGE,
∴EG=GM=AM+AG=AG+CE,设AG=x,则DG=3-x,GE=1+x,
在Rt△DGE中,∵GE2=DG2+DE2,
∴(3-x)2+22=(x+1)2,
∴x=$\frac{3}{2}$,
∴AG=DG,
易证△AGB≌△DGF,
∴BG=FG=$\sqrt{A{B}^{2}+A{G}^{2}}$=$\frac{3}{2}$$\sqrt{5}$,
∴BF=2BG=3$\sqrt{5}$,
故选B.
点评 本题考查正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
8. 关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
 关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )
关于x的不等式3x-m≥5的解集如图所示,则m的值等于( )| A. | $\frac{4}{3}$ | B. | -1 | C. | -5 | D. | -8 |
9.已知方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,那么方程组$\left\{\begin{array}{l}{{a}_{1}(x-1)+{b}_{1}(y+2)={c}_{1}}\\{{a}_{2}(x-1)+{b}_{2}(y+2)={c}_{2}}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
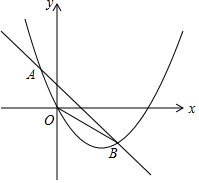 如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,
如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,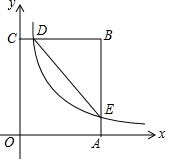 如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.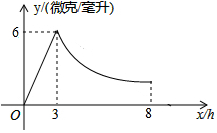 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.
某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.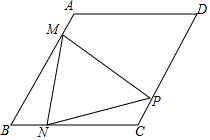 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.