题目内容
16.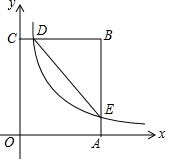 如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.
如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.(1)连接OE,若△EOA的面积为3,则k=6;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
分析 (1)连接OE,根据反比例函数k的几何意义,即可求出k的值.
(2)根据矩形的长和宽及反比例函数y=$\frac{k}{x}$(k>0)表示D和E的坐标,计算tan∠BDE=tan∠CB′B的值相等,所以计算B′C的长,得出D的坐标.
解答  解:(1)连接OE,如图1,
解:(1)连接OE,如图1,
∵Rt△AOE的面积为3,
∴k=2×3=6.
故答案为:6;
(2)连接DB′,
设D($\frac{k}{5}$,5),E(3,$\frac{k}{3}$),
∴BD=3-$\frac{k}{5}$,BE=5-$\frac{k}{3}$,
∴tan∠BDE=$\frac{BE}{BD}$=$\frac{5-\frac{k}{3}}{3-\frac{k}{5}}$=$\frac{5}{3}$,
∵B与B′关于DE对称,
∴DE是BB′的中垂线,
∴BB′⊥DE,BG=B′G,DB′=BD,
∴∠DGB=90°,
∴∠BDE+∠DBB′=90°,
∠CB′B+∠DBB′=90°,
∴∠BDE=∠CB′B,
∴tan∠BDE=tan∠CB′B=$\frac{5}{3}$=$\frac{BC}{CB′}$=$\frac{3}{CB′}$,
∴CB′=$\frac{9}{5}$,
设CD=x,则BD=B′D=3-x,
则${x}^{2}+(\frac{9}{5})^{2}=(3-x)^{2}$,
∴x=$\frac{24}{25}$,
∴D($\frac{24}{25}$,5).
点评 本题考查了反比例函数k的几何意义、图象上点的特征、矩形的性质、特殊的三角函数、轴对称的性质、线段垂直平分线的性质,第三问中熟练掌握轴对称的性质和反比例函数点的坐标特征是关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
4. 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\frac{8}{3}$$\sqrt{10}$ |
11.已知x为任意实数时.函数y=x2+|x-a|+1的最小值为$\frac{7}{4}$,则实数a的值( )
| A. | 1,-$\frac{1}{2}$ | B. | 1,-1 | C. | -1 | D. | $\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{6}}{2}$ |
8.对于反比例函数y=$\frac{3}{x}$,当x>1时,y的取值范围是( )
| A. | 0<y<3 | B. | y>3或y<0 | C. | y>3 | D. | 以上答案都错 |
5.在①平行四边形,②矩形,③菱形,④正方形中,既是轴对称图形,又是中心对称图形的是( )
| A. | ①②③④ | B. | ②③ | C. | ②③④ | D. | ①③④ |
 .
.