题目内容
14.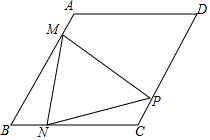 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.(1)当t=2时,∠NMP=30度;
(2)求t为何值时,以A、M、C、P为顶点的四边形是平行四边形;
(3)当△NPC为直角三角形时,求此时t的值.
分析 (1)如图1中,连接AC.t=2时,AM=BM=2,BN=CN=2,由PM⊥AB,可得PA=PB,推出P与C重合,由MN∥AC,推出∠NMP=∠ACM=$\frac{1}{2}$∠ACB=30°;
(2)若点P在线段CD上时,过A作AE⊥CD于E,想办法构建方程即可解决问题;
(3)若点P在线段CD上时,不存在Rt△NPC,只有当P在线段DC延长线上时,才存在Rt△NPC,分两种情形讨论求解即可;
解答 解:(1)如图1中,连接AC.
∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,
∴△ABC,△ACD都是等边三角形,
∵t=2时,AM=BM=2,BN=CN=2,
∵PM⊥AB,
∴PA=PB,
∴P与C重合,
∵MN∥AC,
∴∠NMP=∠ACM=$\frac{1}{2}$∠ACB=30°.
故答案为30.
(2)若点P在线段CD上时,过A作AE⊥CD于E,
在菱形ABCD中,AB∥CD,∠D=60°,AB=AD=CD=BC=4
∴DE=$\frac{1}{2}$AD=2,AE=2$\sqrt{3}$,
∴AM=t,PC=2-t
要使四边形AMCP为平行四边形,则AM=PC
∴t=2-t得t=1.
若点P在线段DC延长线上时,四边形AMCP不是平行四边形.
(3)若点P在线段CD上时,不存在Rt△NPC,
∴只有当P在线段DC延长线上时,才存在Rt△NPC,
如图3中,当∠NPC=90°时,则M、N、P在同一直线上,
∴∠CNP=∠MNB=30°,
∴BM=$\frac{1}{2}$BN,即4-t=$\frac{1}{2}$t,
解得,t=$\frac{8}{3}$.
如图4中,当∠PNC=90°时,
易知BG=2(4-t),MG=$\sqrt{3}$(4-t),
GN=t-2(4-t)=3t-8,GP=NG÷cos30°=$\frac{2\sqrt{3}}{3}$(3t-8),
∵PM=2$\sqrt{3}$,
∴MG+GP=2$\sqrt{3}$,
∴$\sqrt{3}$(4-t)+$\frac{2\sqrt{3}}{3}$(3t-8)=2$\sqrt{3}$,
解得t=10,不合题意,
综上所述,t=$\frac{8}{3}$s时,△PNC是直角三角形.
点评 本题考查菱形的性质、等边三角形的判定和性质、锐角三角函数、直角三角形30度角性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.

 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\frac{8}{3}$$\sqrt{10}$ |
| A. | ①②③④ | B. | ②③ | C. | ②③④ | D. | ①③④ |

| A. | 8$\sqrt{2}$ | B. | 12 | C. | 4$\sqrt{2}$ | D. | 6 |
 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )| A. | ∠1=180°-∠3 | B. | ∠1=∠3-∠2 | C. | ∠2+∠3=180°-∠1 | D. | ∠2+∠3=180°+∠1 |
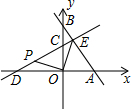 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.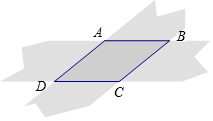 如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为4$\sqrt{2}$.
如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为4$\sqrt{2}$.