题目内容
19.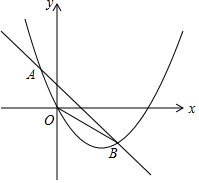 如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,
如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,(1)求m与n之间的数量关系;
(2)若OA=OB,求该抛物线和直线的解析式.
分析 (1)将A与B的坐标代入抛物线中即可求出m与n的关系式;
(2)由于OA=OB,从而可知$\frac{1}{4}$+m2=1+n2,由(1)中m与n的关系式即可求出m与n的值,从而可求出点A的坐标,利用待定系数法即可求出b的值.
解答 解:(1)将A(-$\frac{1}{2}$,m),B(1,n)代入y=x2-bx,
∴m=$\frac{1}{4}$+$\frac{b}{2}$,n=1-b,
将b=1-n代入m=$\frac{1}{4}$+$\frac{b}{2}$,
∴2m+n=$\frac{3}{2}$
(2)∵OA=OB
∴OA2=OB2
∴$\frac{1}{4}$+m2=1+n2
∴$\left\{\begin{array}{l}{2m+n=\frac{3}{2}}\\{{m}^{2}-{n}^{2}=\frac{3}{2}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=1}\\{n=-\frac{1}{2}}\end{array}\right.$
∴A(-$\frac{1}{2}$,1)
将A(-$\frac{1}{2}$,1)代入y=x2-bx,
∴1=$\frac{1}{4}$+$\frac{b}{2}$
∴b=$\frac{3}{2}$
∴抛物线的解析式为:y=x2-$\frac{3}{2}$x
点评 本题考查待定系数法,解题的关键是熟练运用待定系数法,本题属于中等题型.

练习册系列答案
相关题目
14.已知二次函数y=ax2-bx+0.5b-a与x轴交于A、B两点,则线段AB的最小值为( )
| A. | 0.5 | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
4. 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\frac{8}{3}$$\sqrt{10}$ |
11.已知x为任意实数时.函数y=x2+|x-a|+1的最小值为$\frac{7}{4}$,则实数a的值( )
| A. | 1,-$\frac{1}{2}$ | B. | 1,-1 | C. | -1 | D. | $\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{6}}{2}$ |
8.对于反比例函数y=$\frac{3}{x}$,当x>1时,y的取值范围是( )
| A. | 0<y<3 | B. | y>3或y<0 | C. | y>3 | D. | 以上答案都错 |
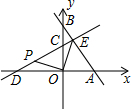 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.